用补形法解立体几何题
来源:未知发布时间:2017-06-24
几何体的补形要围绕着已知条件来进行,通常策略是把棱锥补成棱柱,把台体补成锥体,把三棱锥补成四棱锥,把三棱柱补成四棱柱,把不规则几何体补成规则几何体,补同样几何体等。
一、棱锥补成棱柱
例1、一个四面体的所有棱长都为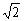 ,四个顶点在同一球面上,则球的表面积为
,四个顶点在同一球面上,则球的表面积为
A. 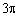
B. 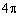
C. 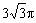
D. 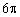
分析:正四面体可看作是正方体经过切割而得到,因而构造一个棱长为1的正方体ABCD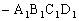 ,则四面体
,则四面体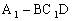 就是棱长为
就是棱长为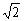 的正四面体,而正方体的外接球就是四面体的外接球,又正方体的对角线长就是球的直径,易知对角线长度为
的正四面体,而正方体的外接球就是四面体的外接球,又正方体的对角线长就是球的直径,易知对角线长度为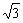 ,故球表面积
,故球表面积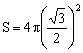
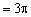 。
。
总结:对棱长全相等的正四面体通常把它补成正方体。若是相对棱长相等的四面体,则可考虑把它补成长方体。
例2、如图1,在底面是直角梯形的四棱锥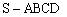 中,∠ABC=
中,∠ABC=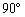 ,SA⊥面ABCD,SA=AB=BC=1,AD=
,SA⊥面ABCD,SA=AB=BC=1,AD=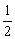 。
。
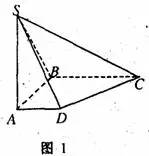
(1)求四棱锥 的体积;
的体积;
(2)求面SCD与面SBA所成的二面角的正切值。
解:(1)解答略。
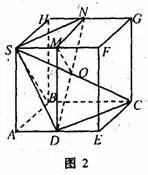
(2)以SA为棱,构造正方体AECB-SFGH,如图2,分别取棱SF、HG中点M、N,连结DM、MN、SN、ND,设ND与SC相交于O,连接MO。
则有面MDN∥面SAB,且SM⊥面MDN,
所以所求的二面角等于二面角S-DN-M。
在正方体AECB-SFGH中,△NSD与△NMD都是等腰三角形,所以SO⊥DN,
MO⊥DN,所以∠SOM是二面角S-DN-M的平面角。又MO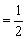 SB=
SB=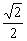 ,SM=
,SM=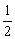 ,所以
,所以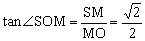 ,故所求二面角的正切值是
,故所求二面角的正切值是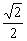 。
。
总结:从一顶点出发的三条棱互相垂直的锥体通常可考虑把它补成长方体或正方体。
二、三棱柱可补成四棱柱
例3 已知斜三棱柱的侧面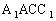 与平面ABC垂直,∠ABC=
与平面ABC垂直,∠ABC=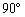 ,BC=2,AC=
,BC=2,AC=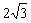 ,且
,且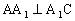 ,
,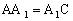 ,求点C到侧面
,求点C到侧面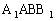 的距离。
的距离。
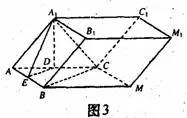
解:把斜三棱柱ABC 补成如图3所示的平行六面体,设所求的距离为d,则d也是平面
补成如图3所示的平行六面体,设所求的距离为d,则d也是平面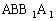 与平面
与平面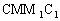 间距离,作
间距离,作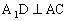 于点D,作
于点D,作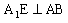 于点F,因为
于点F,因为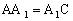 ,
,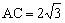 ,
,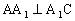 ,所以
,所以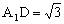 ,又∠ABC=
,又∠ABC=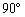 ,BC=2,所以
,BC=2,所以 ,因侧面
,因侧面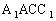 与底面ABC垂直,
与底面ABC垂直,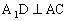 于点D,所以
于点D,所以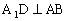 ,又
,又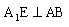 ,知AB⊥面
,知AB⊥面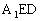 ,因而AB⊥ED,又∠ABC=
,因而AB⊥ED,又∠ABC=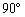 ,所以DE∥BC,D为AC中点,且
,所以DE∥BC,D为AC中点,且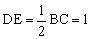 ,故
,故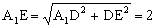 ,而
,而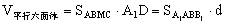 。
。
所以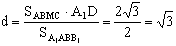 。
。
总结:本例通过斜三棱柱补成四棱柱,从而达到把线面距离转化为面面距离,再通过等积变换达到简化解题之目的。
三、棱台补成棱锥
例4、如图4,三棱柱ABC 中,若E、F分别为AB、AC的中点,平面
中,若E、F分别为AB、AC的中点,平面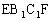 将三棱柱分成体积为
将三棱柱分成体积为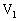 、
、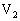 的两部分,那么
的两部分,那么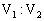 等于多少?
等于多少?
解:延长 到
到 ,
,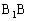 到
到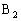 ,
,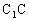 到
到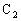 ,且
,且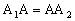 ,
,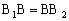 ,
,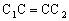 ,则得三棱柱
,则得三棱柱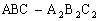 ,且
,且
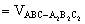 ,延长
,延长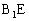 、
、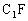 ,则
,则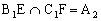 即有三棱锥
即有三棱锥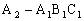 。
。
因为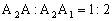 ,所以
,所以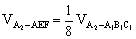 ,又
,又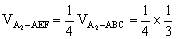
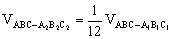 。
。
所以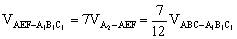 。
。
故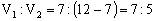 。
。
总结:本题通过把棱台补成棱锥,以棱锥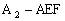 为辅助几何体,利用它与棱柱ABC
为辅助几何体,利用它与棱柱ABC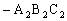 及棱台
及棱台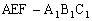 的关系进行变换。
的关系进行变换。
四、补相同几何体
例5、长方体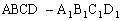 中,AB=
中,AB=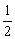 ,AD=1,
,AD=1,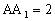 ,求异面直线
,求异面直线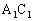 与
与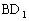 所成的角。
所成的角。
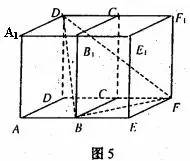
解:如图5,补一个与原长方体全等的并与原长方体有公共面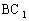 的长方体
的长方体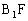 ,连结BF,则∠
,连结BF,则∠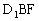 为异面直线
为异面直线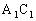 与
与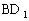 所成的角,而
所成的角,而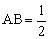 ,AD=1,
,AD=1,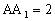 。
。
连结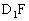 ,在△
,在△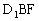 中,BF=
中,BF=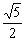 ,
,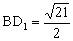 ,
,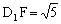 ,由余弦定理得
,由余弦定理得 ,故
,故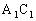 与
与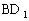 所成角为
所成角为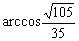 。
。
总结:补相同几何体之目的在于平移相关直线。
五、不规则几何体补成规则几何体
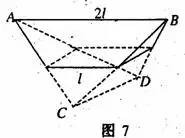
例6、如图6,多面体的底面是边长为l的正方形,上面的棱平行于底面,其长为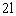 ,其余棱均为l,求这个多面体的体积。
,其余棱均为l,求这个多面体的体积。
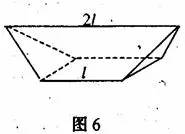
解:如图7,作以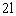 为棱长的正四面体ABCD,连结AC、AD、BC、BD中点组成的四边形为正方形即为多面体的底面(因正四面体的对棱互相垂直),这个正方形所在平面把四面体分成两个全等的多面体,故
为棱长的正四面体ABCD,连结AC、AD、BC、BD中点组成的四边形为正方形即为多面体的底面(因正四面体的对棱互相垂直),这个正方形所在平面把四面体分成两个全等的多面体,故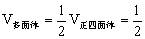
 。
。