一、对勾函数的概念与图像

形如的函数，因为其图像类似于平时的对

勾，因此称这种函数为对勾函数，图像见下图。

当a>0,b>0时，

当a<><>时，

当a,b异号时，函数不是对勾函数，关于此时函数的图像与性质，有机会小数老师再向大家介绍。

二、对勾函数的性质（下面我们只研究a>0,b>0时的情况，其他情况可以根据函数的对称性进行研究。）

1，定义域与值域：

很明显，定义域是；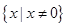

下面研究值域，对于值域的研究，有多种方法，下面小数老师介绍最常用的——均值定理

当x>0时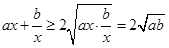，，当且仅当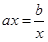时，等号成立，此时；

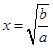当x<>时，，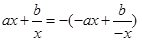

因为x<>，所以-a>0，所以，即，

当且仅当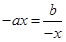时，等号成立，此时；

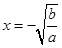所以此函数的值域是：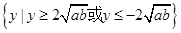

2，顶点：

由（1）可得，两顶点坐标为：

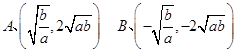
3，单调性：

对于函数单调性的判断，可以利用导数法或者定义法，下面小数老师采用导数法。

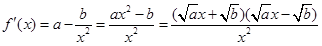
令f’(x)=0，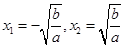

所以

    x

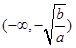
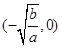
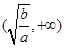
   f’(x)

       +

    -

    -

     +

   f(x)

单调递增

单调递减

单调递减

单调递增

4，奇偶性：

很明显，函数f(x)是奇函数。

5，渐近线：

通过图像，我们可以看到，对于函数f(x)，有两条渐近线，

y=ax,

y=0

函数与这两条直线无限接近，但永不相交。

三、例题

对勾函数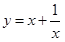具有以下性质：

当x≥1时，y随x增大而增大，

如：2≤x≤4，那么当x=2，y有最小值2+ （1/2）=5/2；

当x=4时，y有最大值为4+（1/4）=17/4.

请根据上述材料，完成以下问题：

（1）       当3≤x≤5时，求函数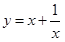的最大值和最小值；

（2）  0≤x≤2时，求函数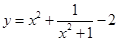的最大值和最小值。