作为河南省中考的热点与难点，二次函数的重要性不言而喻。事实上，作为最基本的初等函数，二次函数既简单又有丰富的内涵和外延，是初高中衔接最紧密的内容之一。

可以以其为基础研究函数的单调性、增减性、最值等性质，也可以结合方程、不等式，甚至是几何图形形成比较复杂的综合性题目。

但从初中学生对它的实际掌握情况来看，许多学生对二次函数的应用掌握得并不是很理想，甚至是“谈函色变”，束手无策。对初中二次函数的认识在很大程度上影响着学生对高中新知识的学习。

距2017中考还有48天，希望本文能对孩子们梳理二次函数相关知识点有所帮助。

中考23题一般考察的是二次函数与几何的综合题型，这里的几何一般有特殊的三角形、特殊四边形的存在性，以及线段及图形的周长与面积的最值。

存在性问题分为两类：一类是静态的，我们可以根据二次函数的对称性以及图形的特点去解决，难度较小；另一类是动态的，关键是要根据题意找出动点在运动过程中一些不变的量或者不变的关系。

接下来从特殊三角形和特殊四边形两个方面梳理一下相关的逻辑思路。

1. 等腰三角形

等腰三角形特性：两腰相等

例如：一次函数与坐标轴分别交于 A 、B 两点，以 AB为边构造等腰△ABC ，C 在坐标轴上。

⑴ AB=AC 时，以 A 为圆心，AB 为半径画圆与坐标轴交点（3 个）

⑵ BA=BC 时，以 B 为圆心，BA 为半径画圆与坐标轴交点（3 个）

⑶ CA=CB 时，AB 中垂线与坐标轴交点（2 个）

 特别提醒 

注意当与轴夹角为特殊角度时，交点有重复的情况▼

 做等腰三角形存在性问题 

①先用两圆一垂的思路梳理出答案有几种情况；

②根据动点所在图象的关系式设出点坐标；

③分类讨论按照两点距离公式求出未知数的值。

2. 直角三角形

直角三角形特性：①三垂直相似；②直角边 k 值乘积为 -1 ；③勾股定理

做直角三角形存在性问题时，根据题意判断谁可以为直角顶点，根据动点所在图象的关系式设出点、坐标，分类讨论列出方程求出未知数的值。

3. 等腰直角三角形

等腰直角三角形特性：等腰三角形和直角三角形的综合。

 分为以下两种：

⑴ 较为简单的一种等腰直角三角形的存在性是三角形一边确定，只有一个动点，此时可以构成等腰直角三角形的点参考下图（6 个）。

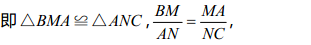
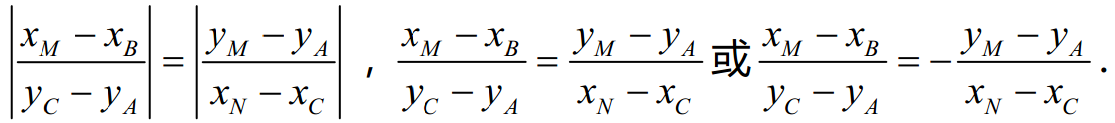
上述三种特殊三角形的存在性审题一定要注意分析清楚题目当中所给的条件，看动点在坐标系中的 位置是否是相对确定的，这样我们在用所设坐标去表示线段长度的时候才不会出纰漏。

4. 相似（全等）三角形

相似三角形的存在性分为两种：直角三角形和一般三角形。

⑴ 直角三角形本身就有一个直角相等，所以直角三角形的相似只需要再找一个锐角相等或者两组边对应成比例，锐角相等我们也可以借助三角函数值转化为线段比例相等。

最后还有一个细节很重要，E 为直线 AC 上方抛物线上一点，所以相应地点 E 横坐标注意取值范围。

⑵ 一般三角形相似，需要先确定两个三角形中的某一组角度相等，再去证明该组角的两组邻边对应成比例。

二、特殊四边形存在性

在这里所说的特殊四边形是平行四边形系列。因为平行四边形对角线互相平分，所以坐标系中的平行四边形存在一个很重要的性质。

已知坐标系内平行四边形 ABCD ，对角线 AC 、BD 交于 M 。

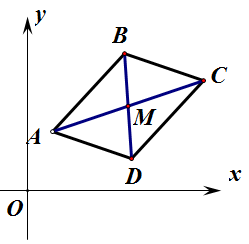
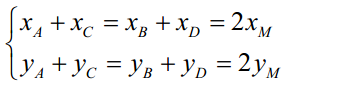
坐标系内特殊四边形的存在性问题很多都是借助这一性质来解决问题。

1. 平行四边形 

作为平行四边形系列最普通的图形，平行四边形的存在性问题主要分为下列两种：

⑴ 三定一动

已知坐标系内 A 、B 、C 三点坐标，确定平行四边形第四个顶点的坐标。

⑵ 两定两动

为保险起见，确定两动点之后可检验是否有三点共线的情况需排除。

2. 菱 形 

作为一种特殊的平行四边形，在考虑菱形存在性问题的时候也可以在平行四边形存在性的基础之上添加一些限定条件，如邻边相等（两点距离公式）或者对角线互相垂直（ k1 · k2 =-1 ）。

这是四个顶点是已知或者在明确的图象上的时候可以参考的方法，但在做题的时候一般菱形的存在性是两定两动的情况， 并且其中一个动点还是在坐标系中不确定具体的位置。

 例如▼

坐标系中直线 AB 和抛物线交于点 A、B，且点 B 是抛物线的顶点。M 是直线 AB 上一动点，在平面直角坐标系内是否存在点 N ，使 以 O、B、M、N 为顶点的四边形是菱形。

 思路▼

菱形任意三个顶点所构成的三角形一定是等腰三角形，所以这道题实质上是 △MOB 为等腰三角形，设点 M 坐标，分类讨论（参考等腰三角形存在性）求出未知数，之后再利用中点公式求出点 N 坐标。

3. 矩 形 

和菱形类似，矩形可以在平行四边形的基础之上添加一组邻边垂直（ k1 · k2 =-1 ）或对角线相等（两点距离公式）

 例如▼

4. 正方形

正方形是最特殊的平行四边形，在大多数情况下，其实正方形和等腰直角三角形是共通的。所以在做题的时候遇到以坐标系内某条线段为边构造正方形的时候，和等腰直角三角形的存在性是一样的。（参考之前等腰直角三角形存在性）就不做过多赘述。

坐标系内特殊三角形和特殊四边形的存在性问题，首先要把握好题目中所给的信息，按边或者角度分类讨论的时候勿遗漏情况。当然有时候也要结合动点坐标的取值范围舍掉一些情况。

特殊图形存在性思路其实并不是很难，但计算量不小，计算的时候要细心一些。

三、函数中的线段

作为图形最基本的组成部分，线段在函数问题中当然也起着不可或缺的重要作用。初中阶段所能够遇到的线段问题主要分为（单）线段最值和线段比例问题。

1. 点到直线的距离

一次函数与坐标轴分别交于 A、B 两点，C 为直线 AB 外一点，求点 C 到 直线 AB 的距离。

2. 铅垂高

如图，所谓铅垂高，就是直线 AB 外一点 C ，过点 C 作 x 轴的垂线分别交直线 AB 和 x 轴于 E 、 D ， CE 即为点 C 与直线 AB 的铅垂高。

3. 线段比例问题

涉及到线段比例问题，在初中阶段一般情况下都是把线段比转化成两个线段端点的横纵坐标的差之比，主要问法有以下两种：

注意：线段问题一般情况下动点的位置都不确定，需要分类讨论，所以在列等式的时候可以加上绝对值，这样可以避免遗漏情况。

4. 焦点准线问题

二次函数是贯穿初高中的学习，有时候会把高中的某些简单知识点下放，焦点准线问题就其中之一。主要考察的是抛物线上任意一点到某定点的距离和到定直线的距离的不变关系。

抛物线上任意一点到焦点的距离等于到准线的距离。若直线直线 L不是准线，还可以研究丨PM—PN丨为定值。

四、函数中的角度

角度问题是函数中的一个难点，但它和前面的三角形存在性是联系着的，所以特殊角度可以转化为特殊三角形存在性，角度相等可以转化为全等或相似。另外，与三角函数值的结合也是一个很重要的知识点。

 注意：

初中阶段所学习的是锐角三角函数，所以图象与 x 轴夹角咱们一般按锐角的角度来计算，所以由特殊角度的正切值与一次函数的 k 值转化时注意图象走向。

角度问题还有一个很重要的考点就是直线旋转问题，这也会用到高中一个很重要的知识点，和角公式和夹角公式。

在研究线段绕固定点旋转或者是否存在某个特殊角度的时候可以用这两个公式来进行推导。

五、函数中周长与面积

函数中的周长与面积的有很多类型，关键是要根据题目中的信息找到周长和面积的表达式。

1. 周长

初中阶段主要研究几何图形周长的最值，分为最大值和最小值两种。

周

长

最

大

值

周

长

最

小

值

周长最小值时要找线段和的最小值，一般情况下是考虑将军饮马问题。

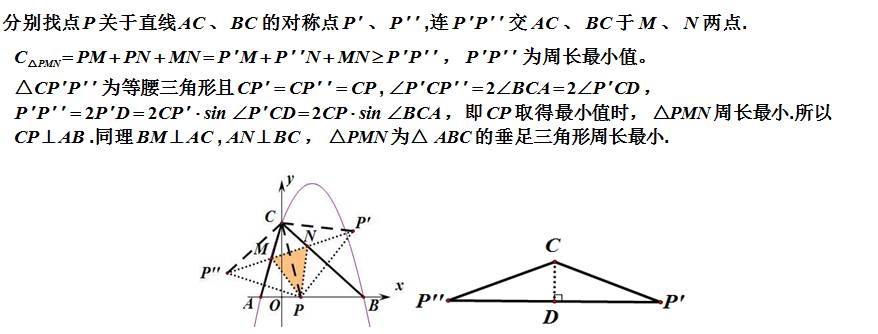
还有一种是将军饮马问题的升级版本，就是在固定三角形三边上各找一个动点构成三角形,使得新组成的三角形周长最小。 

 例如▼

 思路▼

2. 面积

面积问题是函数中的常考题型，通常所让求的图形都不是很特殊的图形，需要借助整体减部分、割补法或者铅垂线法求得面积的表达式。

面积最值和定值

配方求最值:

规律：铅垂高最大的时候面积最大

面积定值和面积最值解题思路是一样的，让面积的表达式是等于定值解方程，但在面积定值问题里一般点 M 和直线 BC 的位置关系不确定，铅垂高表达式需加绝对值。

面积相等

老师有话说

函数的内容重在理解，只有思路清晰在做题的时候才能无往而不利，并且不单单是中考，初中阶段的二次函数综合题还是新高一进一步学习函数的基础。所以即使中考之后，希望大家也要好好梳理二次函数的内容。三年磨一剑，预祝大家中考顺利！

声明：

本文由学而思培优郑州分校初中教研组张龙老师编写，刘国栋老师校阅，转载请注明出处，谢谢！

精彩

推荐

2017郑州二模试卷分析物理、化学点击查看数学点击查看

如果您有任何疑问和想法请在右下角写留言！小编会尽快为您解答的！

如果这篇文章对您有帮助，

请分享给更多有需要的家长！