几何体表面最短路线(1):正方体和长方体(初二数学)
来源:未知发布时间:2017-06-30
几何体表面最短路线是一类 很常见的 题型,其理论依据是:
两点之间线段最短(或垂线段最短)。
需要注意的是:
这个理论依据的前提是在“同一平面内”,因此这类问题的一般处理方式是将空间问题转化为平面问题,将几何体展开后铺在同一平面内进行研究。
例 (1)如图1,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点c’的最短距离是()
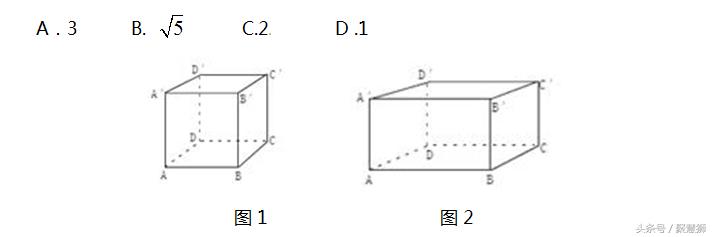
(2)如 图2,有一个长为5,宽为3,高为4的长方体,一只蚂蚁要从A点走到C’点处,怎样走最短?
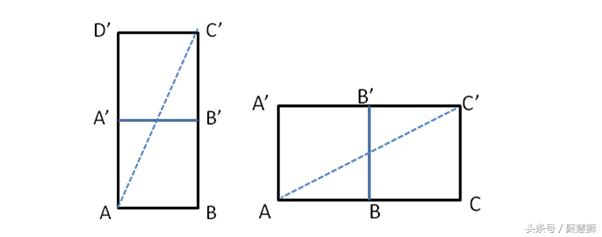
解析:(1)由于正方体的6个面都是同样大小的正方形,因此我们要将点A和点B放到同一个平面里,可以多种不同的展开方式,并且这几种展开方式得到的结果都是一样的。
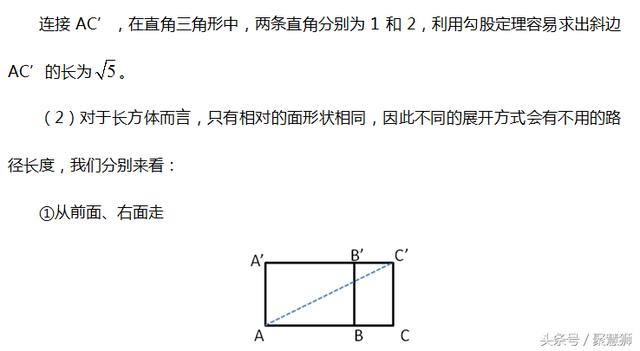
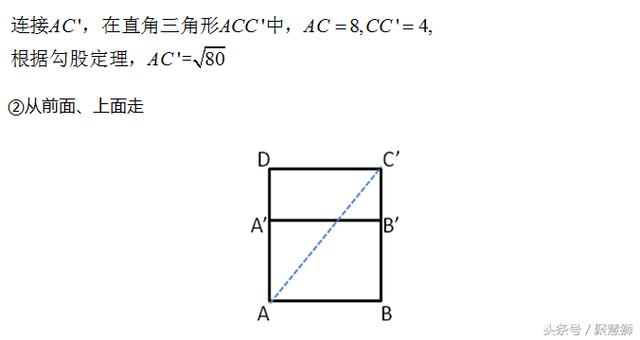
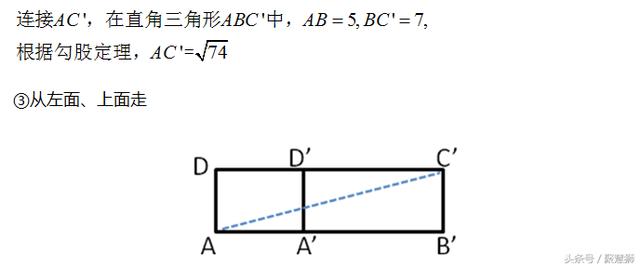

由于长方体有多种邻面展开方式,因此要对所有可能的情况分类讨论,比较得出最短路径。那么是否可以不通过计算直接得到最短路径的展开方式呢?通过观察,我们可以发现:在长方体表面找最短路径,把长方体的相邻两个面展在同一平面时,当所构成的三角形中,最长的棱独立作为直角三角形的一条直角边时,这样的路径最短。同学们不妨自己验证一下。