与中点有关题型方法大总结——初二数学几何考点难点破局
来源:未知发布时间:2017-06-30
初二数学中,与中点有关的几何题,甚至难题,经常成为考试出题老师手中的法宝。今天姚老师就把这类题型的解题方法,逐一归纳总结如下:
【技法一:构造斜边上的中线】

总结:
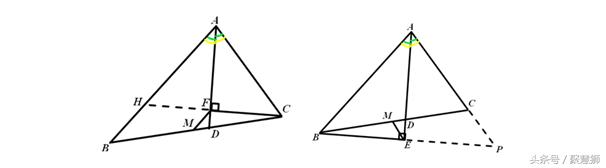
在试题中,常见如图所示的图形,让我们证明标红的两条线段相等或已知标红的线段 相等 ,求证其他的问题,这个时候我们可以先构造直角三角形,证明某线段为其斜边上的中线,再应用直角三角形性质求证。

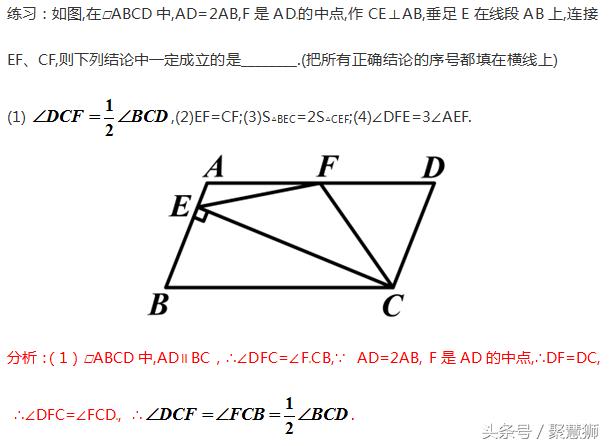
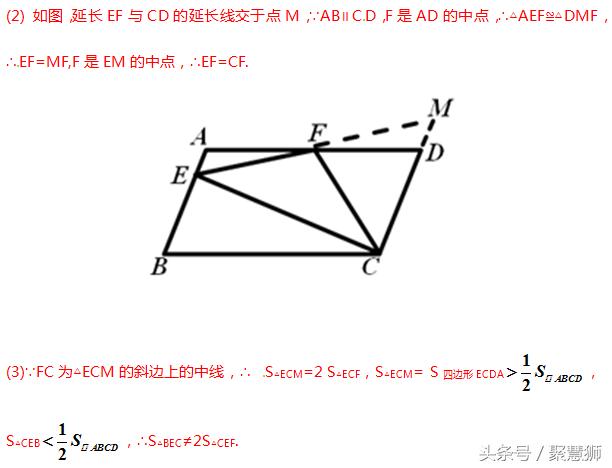

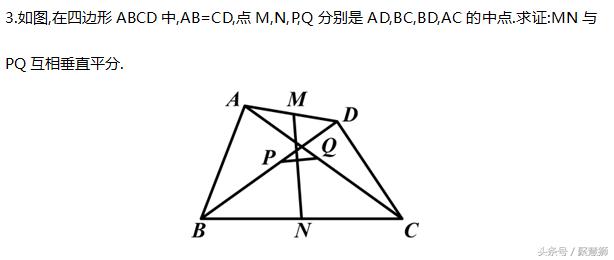
【技法二:构造中位线(已知四边形对边中点)】
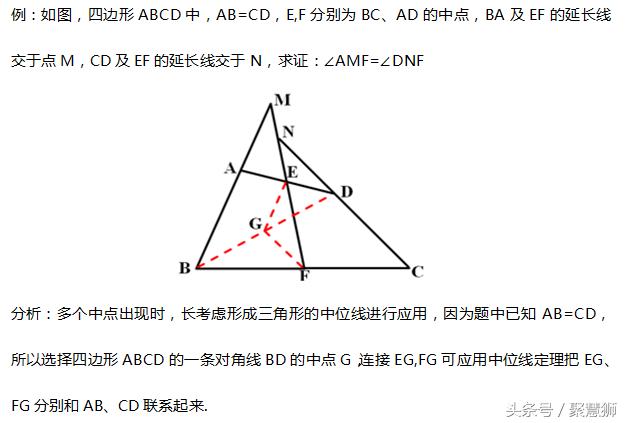

总结:
根据题中的条件选择:
(1)若给出四边形另外一组对边中的信息,选择一条对角线的中点;
(2)若给出的是有关对角线的信息,选择另一组对边中的某条边的中点;
则可以构造出两个三角形的中位线,分别使用中位线定理和题中的条件即可解决!
拓展:
若给出的是四边形两条对角线的中点,这个时候要选择四条边中的一条边的中点构造三角形的中位线!
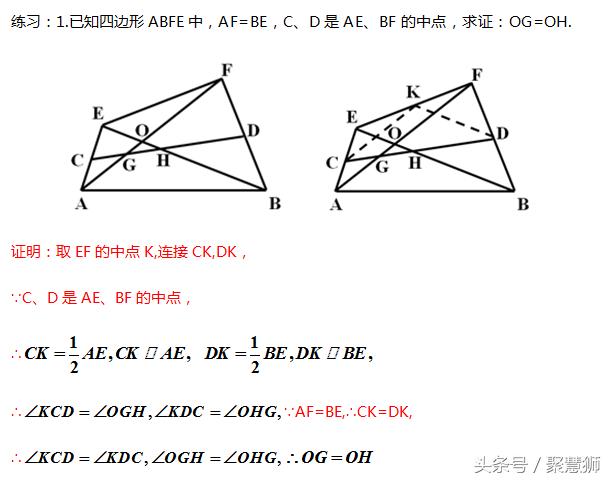
[注释:上面那个平行四边形符号,应该平行符号,表示平行的意思,我电脑里面敲不出来:)暂时替代下]
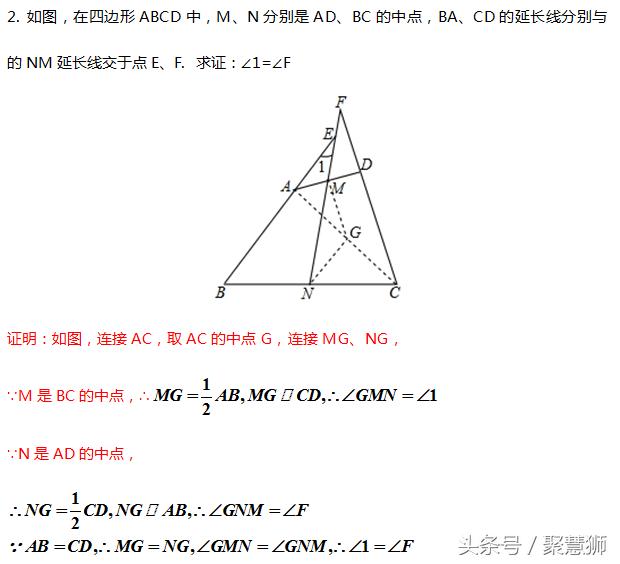
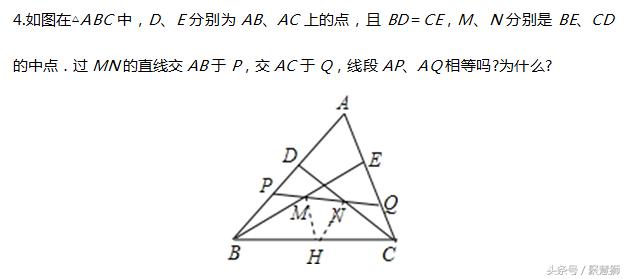

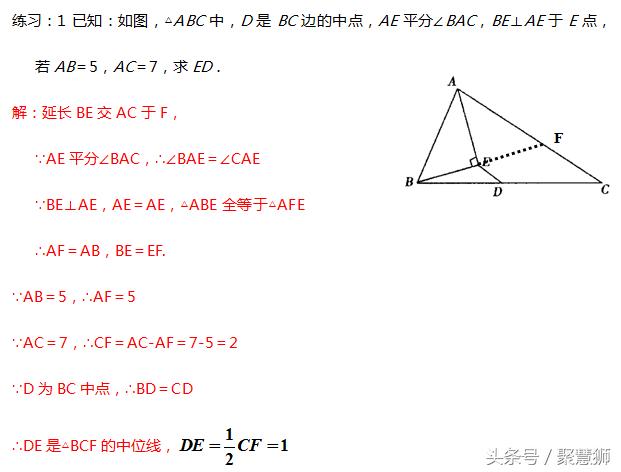
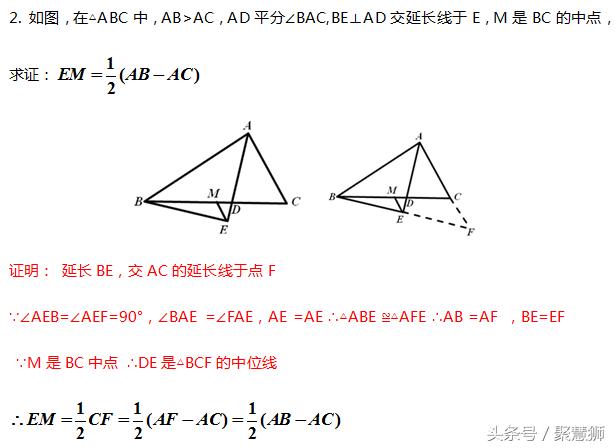
【技法三:构造中位线(与等腰三角形综合)】

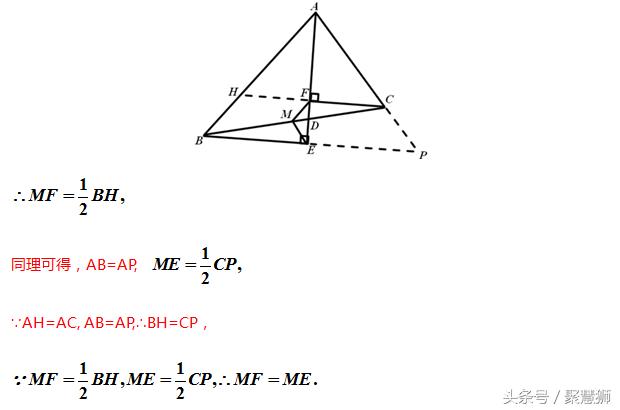
总结:
(1)出现角平分线以及垂直于角平分线的线,常考虑等腰三角形的形成;
(2)当题目的条件中出现三角形一边的中点时,长考虑构成三角形的中位线来应用;
综合考查时,构造等腰三角形,形成中位线,如图