一、的最值

若A为椭圆内一定点（异于焦点），P是C上的一个动点，F是C的一个焦点，e是C的离心率，求的最小值。

例1、已知椭圆内有一点A（2，1），F是椭圆C的左焦点，P为椭圆C上的动点，求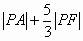的最小值。

分析：注意到式中的数值“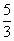”恰为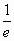，则可由椭圆的第二定义知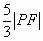等于椭圆上的点P到左准线的距离。答案为。

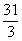二、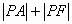的最值

若A为椭圆C内一定点（异于焦点），P为C上的一个动点，F是C的一个焦点，求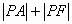的最值。

例2、已知椭圆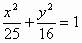内有一点A（2，1），F为椭圆的左焦点，P是椭圆上动点，求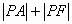的最大值与最小值。

解：如图1，设椭圆的右焦点为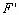，可知其坐标为（3，0）

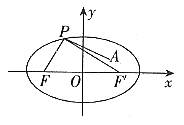
图1

由椭圆的第一定义得：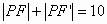

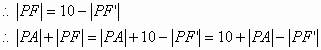
可知，当P为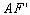的延长线与椭圆的交点时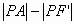，最大，最大值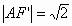为，当P为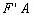的延长线与椭圆的交点时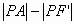，最小，最小值为。

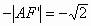故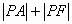的最大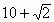值为，最小值为。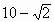

三、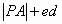的最值

若A为椭圆C外一定点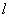，为C的一条准线，P为C上的一个动点，P到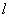的距离为d，求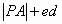的最小值。

例3、已知椭圆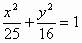外一点A（5，6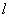），为椭圆的左准线，P为椭圆上动点，点P到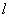的距离为d，求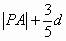的最小值。

解：如图2，设F为椭圆的左焦点，可知其坐标为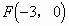

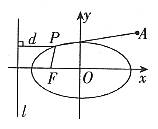
图2

根据椭圆的第二定义有：，即

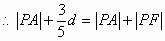
可知当P、F、A三点共线且P在线段AF上时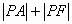，最小，最小值。

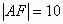故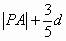的最小值为10。

四、椭圆上定长动弦中点到准线距离的最值

例4、定长为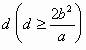的线段AB的两个端点分别在椭圆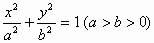上移动，求AB的中点M到椭圆右准线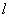的最短距离。

解：设F为椭圆的右焦点，如图3，作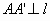于A”，BB”⊥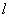于B”，M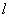M”⊥于M”

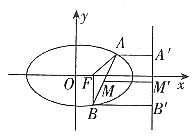
图3

则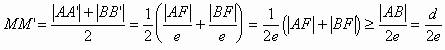

当且仅当AB过焦点F时等号成立。

故M到椭圆右准线的最短距离为。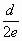

注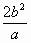：是椭圆的通径长，是椭圆焦点弦长的最小值，是AB能过焦点的充要条件。