以下是初中比较有难度的初中数学选择题，我把整个我们思维的过程，试错的过程记录下来。希望能给予孩子们做为参考，希望他们思考一个问题会有错误的思考，也会有没有用的思考，没有人一下子就能马上做对每个题目，都是在不断的探究过程中摸索出来的，而这种探究思维，这种数学精神，正是IB需要的，这种表达方式也是IB学习需要的。我建议给初中的孩子看看，如果能够打印出来，更加好，我相信给予孩子有些不一样的感觉。问问他们是否有不一样的感受。

思维分析：

当我们遇见这样的题目的时候，我们如何思考？如何开始我们的分析？

下面我介绍一种分析方式。

叫步步定量分析法

基本思路是：从已知条件出发，一句话一句话的读出其中的信息。确定其范围，慢慢缩小可能性，最后得出解题思路。

好的，我们使用上面的这个例子来分析。

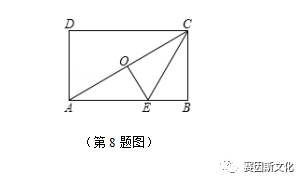
首先读取第一句题目文字“点O是矩形ABCD的中心”这句话告诉我们他这个是矩形，矩形大家知道可能是长方形，或者是长方形的特殊情况正方形。所以出现了模糊情况，这不是一个定量描述。

第二句，E是AB上的点，这句话告诉我们点E可以在AB上动来动去。

第三句，沿着CE折叠之后，点B恰好与点O重合。这句话信息量很大，背后隐藏的东西很多。我们做个实验，你可以试着用纸张或者在草稿纸上画看看，随意的长方形，很难使得点B折叠后恰好与点O重合。那是什么东西决定着点B和点O能重合呢？这个疑问我们留着。读读接下来的条件我们再分析。

第四句，若BC=3，这话是一个定量的具体条件，直接导致我们知道我们能在纸上画出一个确定的矩形的一边，BC边长度是3，这是毫无疑问的。那么我们推断，BC边长确定了，但是矩形另外的边长AB没有定啊？（意思是说我们不知道他有多少长度,心里想，要是知道他的长度也许会对我们分析有帮助）

好，我们在结合起来一起看问题。我们经常要使用的技能是，要把不确定的东西通过分析一步步的确定起来。这是通过分析推理得出来的。

我们从疑点出发，第三句话的疑点是，什么东西决定着B和O重合？第四句，如何确定AB长度？这两个疑问会不会存在关联呢？

我们分析，如果调试AB长度达到适合的位置，是否存在一种情况是使得点O刚好与点B折叠后重合。我们可以知道，这是明显的，肯定存在一种特殊情况符合这种情况。但是我们又不知道到底是多少的时候，符合。这种我们经常使用的解决方式就是方程法。方程可以使得我们算出，符合题目要求的特殊值。但是我们先别这样做先，我们看看是否还有新的发现。

折叠这个词汇包含一个信息，我们需要挖掘。那就是折叠后，CB=CO，角B等于角度COE=90度。

CB定了，那么OC和OA都是定了，都是等于3。哦，这下好了。对角线已经定了，又有一条边确定了，这个三角形或者矩形就确定了。三角形或者矩形定了，意味着AB肯定是可以计算出来的。点E的位置也是肯定可以计算出来的。因为折叠的方法只有一种。只是我们现在不知道是多少而已。这我们肯定可以通过方程式来计算出来的。（一般都是这个方法的）

这时候，我们标记数据进入图形中，观察，发现在三角形CAB中，CB=3，AC=6，而且是斜边和直角边的关系，那么我们依照过去的经验，马上判断出角度CAB为30度，进一步推理出来，角度ACB等于60度，咦，突然发现CE刚好平分角度ACB。马上得出，60除以2等于30度。马上把这些信息标记在图形里。

观察题目的问题是求出CE长度，CE是两个全等直角三角形的斜边。我们想到了勾股定理来解决。但是发现，我们不知道OE或者EB长度，无法用勾股定理直接计算出来。

但是我们上面已经知道角度OCE等于30度，是个特殊角度。性质是直角边等于斜边的一半，但是现在直角边还是不告诉我们，怎么办呢？

这种情况下我们可以使用几种方法来解决，计算出OE或者EB。

第一种，方程法。设OE为未知数x，建立方程组。为何我们使用方程法呢？是因为我们知道了三角形ACB的大小，所以敢肯定OE是可以计算出来的，也就是点B折叠后得到和O重合这个条件可以建立方程，把描述性语言翻译成为数学符合关系式就是建立方程的根本思想。

假设OE为X则，CE就是2X,原因是角度OCE是30度。通过勾股定理可以建立方程。

3的平方加上X的平方，等于2X的平方。解方程会得出X等于正负根号3。排除负数不符合实际长度的表达方式，剩下根号3=X.那么CE自然等于OE的两倍啦，于是CE=2乘以根号3.选择答案A.

方法二，我使用相似三角形的性质来分析。任何的30度直角三角形都是初级30度对应的直角边边长为1的长度的相似三角形。 这个初级原始30度直角三角形我们称为原始30度直角三角形。既然是相似三角形，那么就是意味着从原始三角形扩大n倍得到的三角形，如果n是大于1的数，那么是增大的，如果n小于1则是依照比例边长减少的。原始三角形的边长可以计算出来，三个边长分别为1,2，根号3.记住这是要经常用到，能记住最好，但是也要知道是如何计算出来的。意思是说，任何比这个原始30度直角三角形大的30度直角三角形，都是这个原始三角形的边长的倍数。

分析本题目，分析已知边长OC对应原始30度直角三角形的根号3那条边长，意思是这个三角形从原始三角形扩大N倍数得到的，但是N是多少？我们需要计算。建立一个小方程算式，即：根号3的N倍=OC=3。求出N是根号3.也就是说，比原始30度直角三角形每条边长扩大了N倍，依照这个推论，其他边长也是扩大同等倍数。

CE长度是从原始的边长是2扩大了根号3倍得来的。于是有：2乘以根号3=CE

所以得到答案A.

方法三，使用勾股定理和30度角度性质，比例。得出结论。（本方法是和学生探讨好得出，自己没有想到，其实也是非常妙的）

仔细观察，我们发现三角形AOE，OEC,CEB是全等三角形，这是很容易证明的。前提是我们发现CE平分角OCB.计算知道角OCE等于30度情况下。既然三角形全等，那么AE=EC.因为折叠，所以OE=EB.那么AB其实就是等于AE=EB+AE,因为角ECB等于30度，所以CE是EB的2倍，CE=AE,所以AE=2EB,也就是说AB刚好可以分成3等分，其中点E就是在从B点出发的三分之一上，也就是我们只要计算出AB,那么三分之二就是AE,也等于CE.

好，我们开始用勾股定理计算出AB。AC的平方减去CB的平方，等于AB的平方。计算出AB=3倍根号3，刚好等于三段，每段是根号3.其中AE=2倍根号3.等于CE的长度，所以选择A.

第四种方法是使用三角函数解决。欢迎有兴趣的朋友自己玩玩。