初中数学一题多解题

例题一、两个连续奇数的积是323，求出这两个数

方法一、

设较小的奇数为x,另外一个就是x+2

x(x+2)=323

解方程得：x1=17,x2=-19

所以，这两个奇数分别是：

17、19，或者-17，-19

方法二、

设较大的奇数x,则较小的奇数为323/x

则有：x-323/x=2

解方程得：x1=19,x2=-17

同样可以得出这两个奇数分别是：

17、19，或者-17，-19

方法三、

设x为任意整数，则这两个连续奇数分别为：

2x-1,2x+1

(2x-1)(2x+1)=323

即4x^2-1=323

x^2=81

x1=9,x2=-9

2x1-1=17,2x1+1=19

2x2-1=-19,2x2+1=-17

所以，这两个奇数分别是：

17、19，或者-17，-19

方法四、

设两个连续奇数为x-1,x+1

则有x^2-1=323

x^2=324=4*81

x1=18,x2=-18

x1-1=17,x1+1=19

x2-1=-19,x2+1=-17

所以，这两个奇数分别是：

17、19，或者-17，-19

例题二、某人买13个鸡蛋、5个鸭蛋、9个鹌鹑蛋，共用去9.25元；如果买2个鸡蛋，4个鸭蛋，3个鹌鹑蛋，则共用去3.20元，试问只买鸡蛋、鸭蛋、鹌鹑蛋各一个，共需多少钱？

    解：设鸡、鸭、鹌鹑三种蛋的单价分别为x、y、z元，则根据题意，得

   

    分析：此方程组是三元一次方程组，由于只有两个三元一次方程，因而要分别求出x、y、z的值是不可能的，但注意到所求的是的代数和，因此，我们可通过变形变换得到多种解法。

  1. 凑整法

    解1：，得

    ，得

   

    答：只买鸡蛋、鸭蛋、鹌鹑蛋各一个，共需1.05元（下面解法后的答均省略）

    解2：原方程组可变形为

   

    解之得：

 

  2. 主元法

    解3：视x、y为主元，视z为常数，解<1>、<2>

    得，

   

    解4：视y、z为主元，视x为常数，解<1>、<2>

    得

   

    解5：视z、x为主元，视y为常数，解<1>、<2>

    得

   

 

  3. “消元”法

    解6：令，则原方程组可化为

   

   

    解7：令，则原方程组可化为

   

   

    解8：令，则原方程组可化为

   

   

 

  4. 参数法

    解9：设，则

   

    ，得

    ，得

    由<4>、<5>得

   

    即

 

  5. 待定系数法

    解10. 设

   

    则比较两边对应项系数，得

   

    将其代入<1>中，得

   

 

    附练习题

  1. 有大小两种货车，2辆大车与3辆小车一次可以运货15.5吨；5辆大车与6辆小车一次可以运货35吨。求3辆大车与5辆小车一次可以运货多少吨？（答案：24.5吨）

  2. 有甲、乙、丙三种货物，若购甲3件、乙7件、丙1件共需3.15元；若购甲4件、乙10件、丙1件共需4.20元。问若购甲、乙、丙各1件共需多少元？（答案：1.05元）

 

平面几何

在完成一个数学题的解答时，有必要对该题的内容、形式、条件、结论，做进一步的探讨，以真正掌握该题所反映的问题的实质。如果能对一个普通的数学题进行一题多变，从变中总结解题方法；从变中发现解题规律，从变中发现“不变”，必将使人受益匪浅。
“一题多变”的常用方法有：1、变换命题的条件与结论；2、保留条件，深化结论；
3、减弱条件，加强结论；4、探讨命题的推广；5、考查命题的特例；
6、生根伸枝，图形变换；7、接力赛，一变再变；8、解法的多变等。

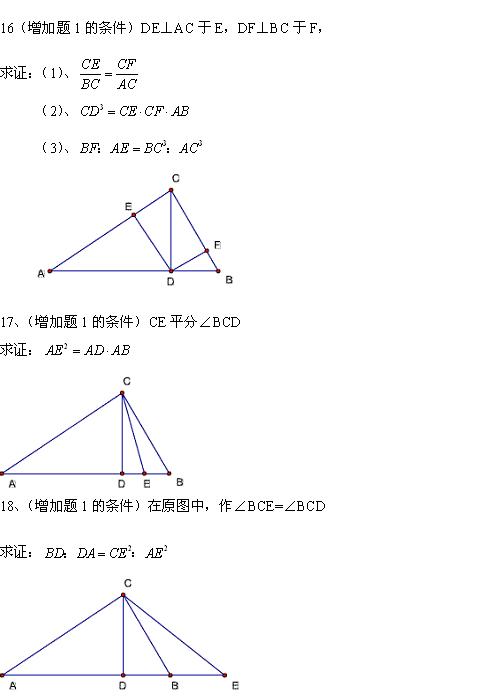
19、（增加题1的条件）AE平分∠BAC交BC于E，
求证：CE：EB=CD：CB

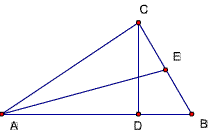
20、（增加题1的条件）CE平分∠BCD，AF平分∠BAC交BC于F

求证：（1）BF·CE= BE·DF

       （2）AE⊥CF

       （3）设AE与CD交于Q，则FQ‖BC

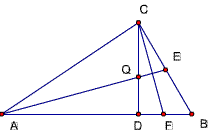
21、已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，以CD为直径的圆交AC、BC于E、F，
求证： CE：BC=CF：AC（注意本题和16题有无联系）

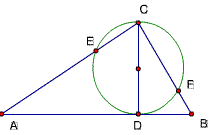
22、已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，以AD为直径的圆交AC于E，以BD为直径的圆交BC于F，

求证： EF是⊙O1和⊙O2的一条外公切线

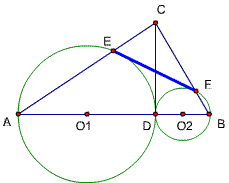
23、已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，作以AC为直径的圆O1，和以CD为弦的圆O2，
求证：点A到圆O2的切线长和AC相等（AT=AC）

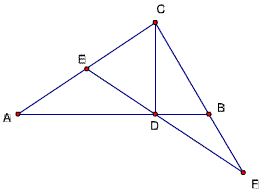
24、已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，
E为ACD的中点，连ED并延长交CB的延长线于F，

求证：DF：CF=BC：AC

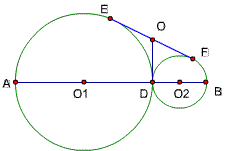
25、如图，⊙O1与⊙O2外切与点D，  内公切线DO交外公切线EF于点O，
求证：OD是两圆半径的比例中项。

 

题14解答：
因为CD^2=AD·DB
    AC^2=AD·AB
    BC^2=BD·AB
所以1/AC^2+1/BC^2
=1/（AD·AB）+1/（BD·AB）
=（AD+DB）/（AD·BD·AB）
=AB/AD·BD·AB
=1/AD·BD
=1/CD^2

15题解答：
因为M为AB的中点，所以AM=MB，AD-DB=AM+DM-(MB-DM)=2DM
AC^2-BC^2=AD*AB-DB*AB
                  =(AD-DB)AB
                 =2DM*AB

 

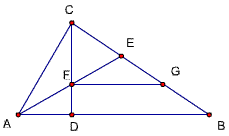
26、（在19题基础上增加一条平行线）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，AE平分∠BAC交BC于E、交CD于F，FG‖AB交BC于点G，
求证：CE=BG

27、（在19题基础上增加一条平行线）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，AE平分∠BAC交BC于E、交CD于F，FG‖BC交AB于点G，连结EG，
求证：四边形CEGF是菱形

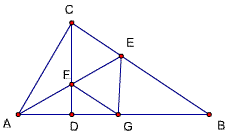
28、（对19题增加一个结论）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，AE平分∠BAC交BC于E、交CD于F，
求证：CE=CF

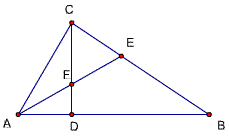
29、（在23题中去掉一个圆）已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，作以AC为直径的圆O1，
求证：过点D的圆O1的切线平分BC

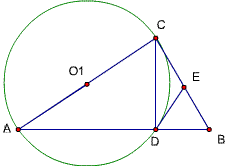
30、（在19题中增加一个圆）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，AE平分∠BAC交BC于E，交CD于F，
求证：⊙CED平分线段AF

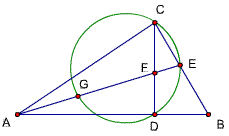
31、（在题1中增加一个条件）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，∠A=30度，
求证：BD=AB/4
（沪科版八年级数学第117页第3题）

32、（在18题基础上增加一条直线）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，作∠BCE=∠BCD
P为AC上任意一点，直线PQ交CD于Q，交CB于M，交CE于N
求证：PQ/PN=QM/MN

 

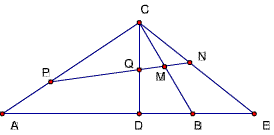
32题证明：
作NS‖CD交直线AC与点S，
则PQ/PN=CQ/SN
又∠BCE=∠BCD
∴QM/MN=CQ/CN（三角形内角平分线性质定理）
∠BCE+∠NCS=∠BCD +∠ACD
NS‖CD，∴∠NSC=∠ACD
∴∠NSC=∠NCS
∴SN=CN
∴PQ/PN=QM/MN

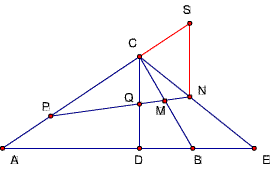
题33
在“题一中”，延长CB到E，使EB=CB，连结AE、DE，
求证：DE·AB= AE·BE

 

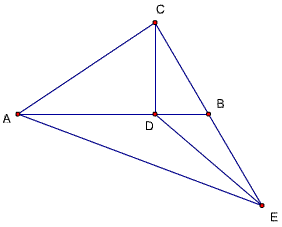
题33证明
CB^2= BD·AB
因EB=CB
∴EB^2= BD·AB
∴EB：BD=AB：BE
又∠EBD=∠ABE
∴△EBD∽△ABE
∴EB：AB=DE：AE
∴DE·AB= AE·BE

 

题34
（在19题基础上增加一条垂线）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，
AE平分CD于F，EG⊥AB交AB于点G，
求证：EG^2= BE·EC

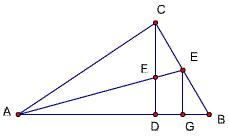
证明：延长AC、GE，设交点为H，
∴△EBG∽△EHC
∴EB：EH=EG：EC
∴EH·EG= BE·EC
又HG‖CD，CF=FD
∴EH=EG
∴EG^2= BE·EC

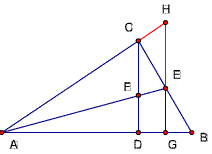
题35（在题19中增加点F）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，
AE平分∠BCA交BC于点E，交CD于F，
求证：2CF·FD = AF·EF

题36、（在题16中，减弱条件，删除∠ACB=90度这个条件）
已知，△ABC中， CD⊥AB，D为垂足，DE⊥AC于E，DF⊥BC于F，
求证：CE/BC=CF/AC

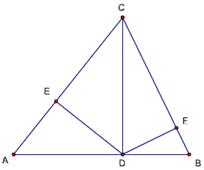
题37
（在题17中，删除∠ACB=90度和CD⊥AB，D为垂足这两个条件，增加D是AB上一点，满足∠ACD=∠ABC）
已知，△ABC中，D是AB上一点，满足∠ACD=∠ABC，又CE平分∠BCD
求证：AE^2= AD·AB

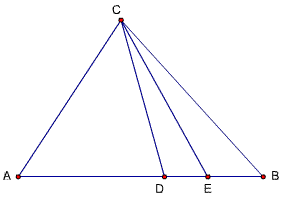
题38
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，PC为⊙ABC的切线
求证：PA/AD=PB/BD

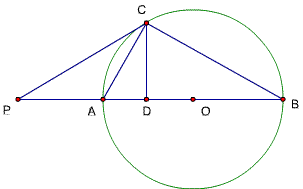
题39
（在题19中点E“该为E为BC上任意一点”）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，
E为BC上任意一点，连结AE，CF⊥AE，F为垂足，连结DF，
求证：△ADF∽△AEB

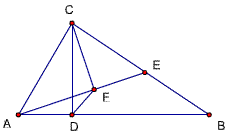
题40：
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足
求证：S⊙ADC：S⊙BDC=AD：DB

题41
已知，如图，△ABC中， CD⊥AB，D为垂足，且AD/CD=CD/BD，
       求∠ACB的度数。

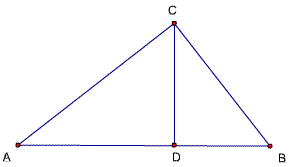
题42
   已知，CD是△ABC的AB边上的高， D为垂足，且AD/CD=CD/BD，
       则∠ACB一定是90度吗？为什么？

题43：
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，△ADC的内切圆⊙O1，
△BDC的内切圆⊙O2，
求证：S⊙O1：S⊙O2=AD：DB

题44：
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，△ADC的内切圆⊙O1的半径R1，△BDC的内切圆⊙O2的半径R2，△ABC的内切圆⊙O的半径R，求证：R1+R2+R=CD

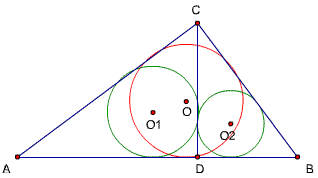
题45、
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，作以AC为直径的圆O1，和以BD为直径的圆O2，设O1和O2在△ABC内交于P
求证： △PAD的面积和△PBC的面积相等

 

题45解：
∠CAP=∠CDP=∠DBP（圆周角、弦切角）
∴Rt△APC∽Rt△BPD
∴AP·PD= BP·PC
又∠APD和∠CPB互补（∠APC+∠BPD=180度）
S △PAD=1/2·AP·PD·sin∠APD
S △PBD=1/2·BP·PC·sin∠CPB
∴S △PAD= S △PBD

 

题46（在题38的基础上变一下）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，PC为⊙ABC的切线，又CE平分∠ACB交⊙ABC与E，交AB与D ，      若PA=5，PC=10，
求   CD·CE的值

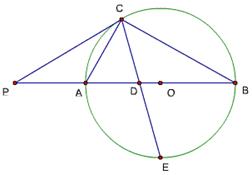
题47
在题46中，求sin∠PCA

题48（由题19而变）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，
AE平分∠ACB交BC于E，EG⊥AB交AB于点G，
求证：（1）AC=AG
（2）、AG^2= AD·AB
（3）、G在∠DCB的平分线上
（4）、FG‖BC
（5）、四边形CEFG是菱形

题49

题49解答：

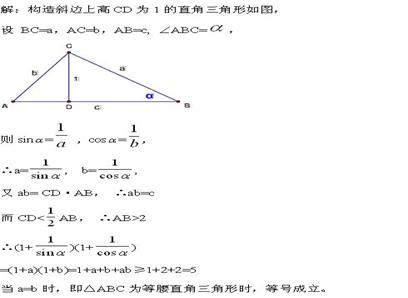
题目50（题33再变）
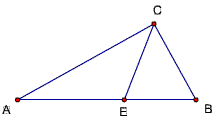
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，延长CB到E，使EB=CB，连结AE交CD的延长线于F，如果此时AC=EC，
求证： AF= 2FE

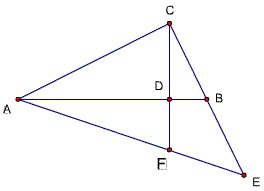
题50解：
过点E作EM⊥CF，M为垂足，则AD：DB=AC^2：CB^2=4：1
又DB：EM=1：2
所以，AD：EM=2：1
△ADF∽△EMF
∴AF：EF=AD：EM=2：1
∴AF=2EF

题目51（题50中连一线）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，延长CB到E，使EB=CB，连结AE交CD的延长线于F，连结FB，如果此时AC=EC，
求证： ∠ABC=∠EBF

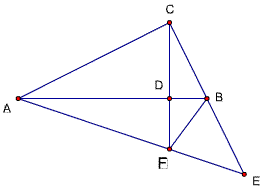
（题51的几种解法）
解法1、
作∠ACB的平分线交AB于点G，易证△ACG≌△CEF
∴CG=EF
∴证△CBG≌△EBF
∴∠ABC=∠EBF

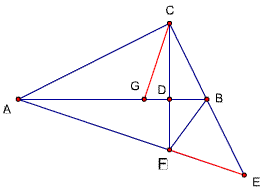
题51解法2
作∠ACB的平分线交AB于点G，交AE于点P，
则点G 为△ACE的垂心，∴GF‖CE
又∠AEC=∠GCE，
∴四边形CGFE为等腰梯形
∴CG=EF
∴再证△CBG≌△EBF
∴∠ABC=∠EBF

题51解法3
作∠ACB的平分线交AB于点G，交AE于点P，
则点G 为△ACE的垂心，
易证△APG≌△CPF（AAS）
∴PG=PF
又∠GPB=∠FPB，
PB=PB
∴△PBG≌△FBP（SAS）
∴∠PBG=∠FBP
∴∠ABC=∠EBF

题51解法4（原题图）
由题50得，AF=2EF
∴AF：EF=AC：BE=2
又∠CAF=∠BEF=45度
∴△ACF∽△EBF
∴∠ACF=∠EBF
又∠ACF=∠CBA
∴∠ABC=∠EBF

 

题51解法5
作ME⊥CE交CD的延长线于M，
证△ABC≌△CME（ASA）
∴∠ABC=∠M
再证△MEF≌△BEF（SAS）
∴∠EBM=∠M
∴∠ABC=∠EBF

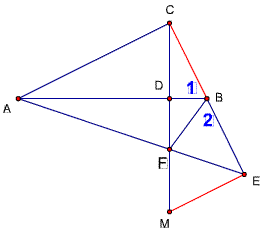
题51解法6
作点B关于点C的对称点N，连结AN，
则NB=2BE，又由题50，AF=2EF，
∴BF‖AN
∴∠EBM=∠N
又∠ABC=∠N（对称点）
∴∠ABC=∠EBF

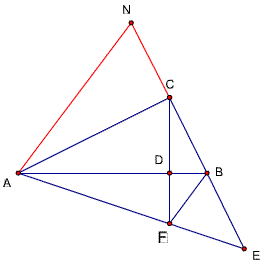
题51解法7
过点C作CH‖BF交AB于M，
∵B为CE的中点，
∴ F为HE的中点
又由题50，AF=2EF，
∴H为AF的中点
又CH‖BF
∴M为AB的中点
∴∠MCB=∠MBC
又∠EBM=∠MCB
∴∠ABC=∠EBF

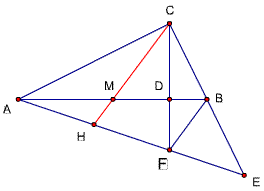
题目52（题50、51结论的引伸）
已知，△ABE中，AC=EC，∠ACE=90度，
CD⊥AB交斜边AB于F，D为垂足，
B为CE的中点，连结FB，
求证：
（1）、AF=2EF
（2）、∠ABC=∠EBF
（3）、∠EBF= ∠E+∠BAE
（4）、∠ABF=2∠DAC
（5）、AB：BF=AE：EF
（6）、CD：DF=AE：AF
（7）、AD：DB=2AF：EF
（8）、CD/DF·FA/AE·EB/BC=1

题目53 （题52的一部分）   
已知如图，
①、AC=CE
②、AC⊥CE
③、CB=BE
④、CF⊥AB
求证：
⑤、AF=2EF
⑥、∠ABC=∠EBF

（题53的14个逆命题中，是真命题的请给出证明）
题目54（题53的逆命题1）
已知如图，
⑤、AF=2EF
②、AC⊥CE
③、CB=BE
④、CF⊥AB
求证：
①、AC=CE
⑥、∠ABC=∠EBF
平面几何一题多变

题目55（题53的逆命题2）
已知如图，
①、AC=CE
⑤、AF=2EF
③、CB=BE
④、CF⊥AB
求证：
②、AC⊥CE
⑥、∠ABC=∠EBF

题目56（题53的逆命题3）
已知如图，
①、AC=CE
②、AC⊥CE
⑤、AF=2EF
④、CF⊥AB
求证：
③、CB=BE
⑥、∠ABC=∠EBF

题目57（题53的逆命题4）
已知如图，
①、AC=CE
②、AC⊥CE
⑤、AF=2EF
③、CB=BE
求证：
④、CF⊥AB
⑥、∠ABC=∠EBF

题目58（题53的逆命题5）
已知如图，
③、CB=BE
⑥、∠ABC=∠EBF
②、AC⊥CE
④、CF⊥AB
求证：
⑤、AF=2EF
①、AC=CE

题目59（题53的逆命题6）
已知如图，
①、AC=CE
④、CF⊥AB
③、CB=BE
⑥、∠ABC=∠EBF

求证：
⑤、AF=2EF
②、AC⊥CE

题目60（题53的逆命题7）
已知如图，
①、AC=CE
②、AC⊥CE
⑥、∠ABC=∠EBF
④、CF⊥AB
求证：
⑤、AF=2EF
③、CB=BE

题目61（题53的逆命题8）
已知如图，
①、AC=CE
②、AC⊥CE
③、CB=BE
⑥、∠ABC=∠EBF

求证：
⑤、AF=2EF
④、CF⊥AB

题目62（题53的逆命题9）
已知如图，
⑤、AF=2EF
④、CF⊥AB
③、CB=BE
⑥、∠ABC=∠EBF

求证：
①、AC=CE
②、AC⊥CE

题目63（题53的逆命题10）
已知如图，
②、AC⊥CE
⑤、AF=2EF
④、CF⊥AB
⑥、∠ABC=∠EBF

求证：
①、AC=CE
③、CB=BE

题目64（题53的逆命题11）
已知如图，
③、CB=BE
⑥、∠ABC=∠EBF
②、AC⊥CE
⑤、AF=2EF
求证：
①、AC=CE
④、CF⊥AB

题目65（题53的逆命题12）
已知如图，
①、AC=CE
⑤、AF=2EF
④、CF⊥AB
⑥、∠ABC=∠EBF

求证：
②、AC⊥CE
③、CB=BE

题目66（题53的逆命题13）
已知如图，
①、AC=CE
⑤、AF=2EF
③、CB=BE
⑥、∠ABC=∠EBF

求证：
②、AC⊥CE
④、CF⊥AB

题目67（题53的逆命题14）
已知如图，
①、AC=CE
②、AC⊥CE
⑤、AF=2EF
⑥、∠ABC=∠EBF

求证：
③、CB=BE
④、CF⊥AB

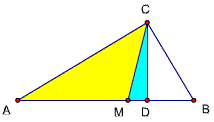
题目68
已知如图，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，
CM平分∠ACB，如果S△ACM=30，S△DCM=6，
求S△BCD=？

（题68解答）
解：
设S△BCD=x,则S△ACM/ S△CMB=30/（6+ x）=AM/MB
S△ACD/ S△CDB=36/ x=AD/DB
又AC^2= AD·AB
BC^2= BD·AB
∴AC^2/ BC^2=AD/BD
∵CM平分∠ACB
∴（AM/ BM）^2=AD/BD
∴[30/(6+x)]^2=36/x
解方程得x=4或x=9
∴S△BCD=4或S△BCD=9

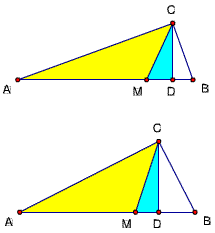
题目69
已知如图，△ABC中，∠ACB=90度，D 为斜边AB上一点，满足AC^2= AD·AB
求证：CD⊥AB

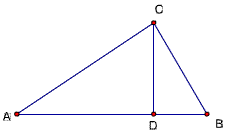
题目70
已知如图，△ABC中，AC>BC,∠ACB=90度，
CM平分∠ACB，且CM+CB=AC，
求证：1/AC-1/BC=√2

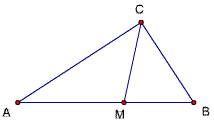
题70证明：
过点M作MD⊥BC，D为垂足，作MD⊥AC，E为垂足，
设ME=x,AC=b,BC=a,则CM=√2 x，AE=b-x,
由AE/AC=ME/BC，得(b-x)/b=x/a,
∴x=ab/(a+b)
又CM+CB=AC
∴√2 x+a=b,
∴ab/(a+b)=(b-a)/ √2
整理得：b^2-a^2=√2ab
两边都除以ab,
∴1/AC-1/BC=√2

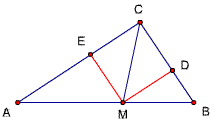
题目71(依题68变)
已知如图，△ABC中（AC>BC），∠ACB=90度，CD⊥AB，D为垂足，
CM平分∠ACB,且BC、AC是方程x^2-14x+48=0的两个根，
求AD、MD的长。

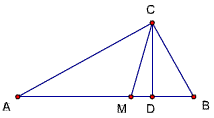
题目71解：
显然，方程x^2-14x+48=0的两根为6和8，
又AC>BC
∴AC=8，BC=6
由勾股定理AB=10
△ACD∽△ABC，得AC^2= AD·AB
∴AD=6.4
∵CM平分∠ACB
∴AM/MB=AC/CB
解得，AM=40/7
∴MD=AD-AM=24/35

题目72
已知如图，△ABC中，∠ACB=90度，AB=2AC，现在将它折成如右图的形状，这时顶点A正好落在BC上，而且△A'MN是正三角形，
求△A'MN与△ABC的面积之比。

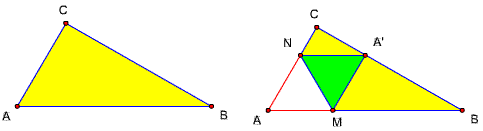
题72解：
∵∠ACB=90度，AB=2AC
∴∠B=30度
由题意，四边形AMA'N是菱形，
∴△A'BM∽△ABC
∴A'M/AC=BM/AB
设AM=x, AB=2AC=2a
∴x/a=(2a-x)/2a
∴x=2a/3
由三角形面积公式，得
S△A'MN：S△ABC=2：9

 

题目73
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足
求证：AB+CD>AC+BC

 

题73的证明：
由三角形面积公式，得AB·CD=AC·BC
2AB·CD=2AC·BC
又勾股定理，得AB^2=AC^2+BC^2
∴AB^2+2AB·CD =AC^2+BC^2+2AC·BC(等式性质)
∴AB^2+2AB·CD =（AC+BC）^2
∴AB^2+2AB·CD+CD^2 >（AC+BC）^2
∴(AB+CD)^2 >（AC+BC）^2
又AB、CD、AC、BC均大于零
∴AB+CD>AC+BC

 

题目74
已知，△ABC中，∠ACB>90度，CD⊥AB，D为垂足
求证：AB+CD>AC+BC

题74证明：如图，作CB’⊥AC交AB于B’,
于是有
AB’·CD=AC·B’C
2AB’·CD=2AC·B’C
又勾股定理，得AB’^2=AC^2+B’C^2
∴AB’^2+2AB’·CD =AC^2+B’C^2+2AC·B’C(等式性质)
∴AB’^2+2AB’·CD =（AC+B’C）^2
∴AB’^2+2AB’·CD+CD^2 >（AC+B’C）^2
∴(AB’+CD)^2 >（AC+B’C）^2
又AB’、CD、AC、B’C均大于零
∴AB’+CD>AC+B’C……①
在△ABB’中,BB’>CB-CB’……②
①+②得AB’ BB’+CD>AC+B’C CB-CB’
∴AB+CD>AC+BC

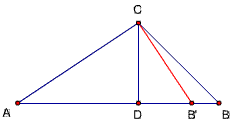
题目75
已知如图，△ABC中， CD⊥AB，D为垂足，
CT平分∠ACB，CM为AB边上的中线，
且∠ACD=∠DCT=∠TCM=∠MCB
求证：∠ACB=90度

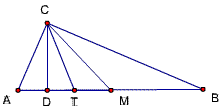
题目75的证明：
延长CT交三角形ABC的外接圆于N，连结MN，
则N为弧AB的中点，所以MN⊥AB，
又CD⊥AB，
∴MN‖CD
∴∠DCT=∠TNM
又∠DCT=∠TCM
∴∠TCM=∠TNM
∴CM=NM
∴CN的垂直平分线必过点M，
又CM为AB边上的中线，MN⊥AB
∴AB的垂直平分线必过点M，
即M为两条弦的垂直平分线的交点，
∴M为三角形ABC的外接圆的圆心，
因此AB为△ABC的外接圆的直径。
∴∠ACB=90度

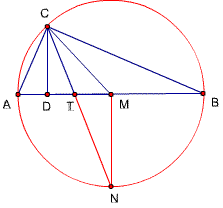
题目76
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，
∠ACB 的平分线CG交AB边上的中垂线于点G ，
求证：MC=MG

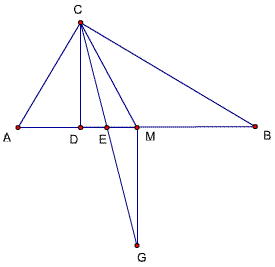
题目77
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，CM为AB边上的中线，CD是∠ACB 的平分线，AC=75cm, BD=80cm,
求CD、CM、CE的长

题目78
  已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，E为⊙ABC上一点，
且弧AC=弧CE，又AE交CD于M，
求证：AM=CM

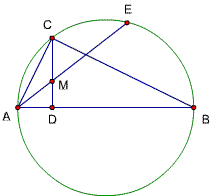
题目79（题78再变）
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，E为⊙ABC上一点，且弧AC=弧CE，又BC交AE于G，连结BE
求证：BG^2= AB·BE- AG·GE

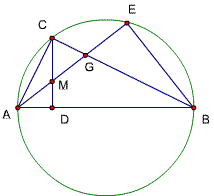
题目80
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，E为⊙ABC上一点，且直线DC于直线BE交于P，
求证：CD^2= DM·DP

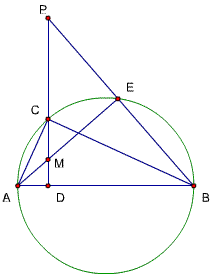
题目81
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，E为⊙ABC上一点，且直线DC于直线BE交于P，如果CD平分AE，
求证： 2DM·DP= BE·EP

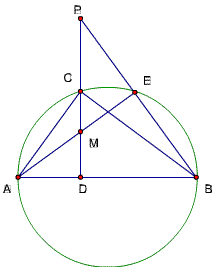
题目82
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，E为⊙ABC上一点，
且弧AC=弧CE，又直线AC与直线BE交于H，
求证： AB=BH

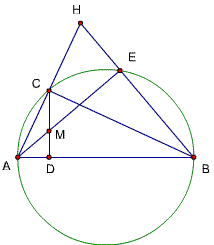
题目83(由题44变)

求证：直角三角形两条直角边的和等于斜边与内切圆直径的和。

 

题目84
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，MN切⊙ABC与C点
求证： BC平分∠DCN

题目85
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，MN切⊙ABC与C点，
AF⊥MN，F为垂足，AE⊥MN，E为垂足，
求证：CD=CE=CF

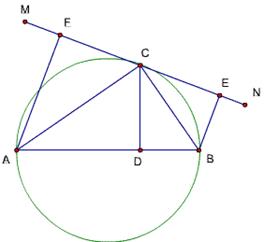
题目86
已知，△ABC中，∠ACB=90度， 以BC为直径的圆交AB于点D，以AC为半径的圆交AB于点E，
求证：∠BCE=∠DCE

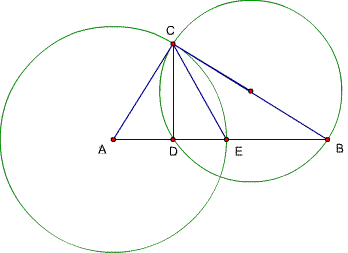
题目87（由题38图而变）
求证：和两定点距离之比等于定比（不为1）的点的轨迹是一个圆周。
（提示：从（1）完备性、（2）纯粹性 两方面来证明。）

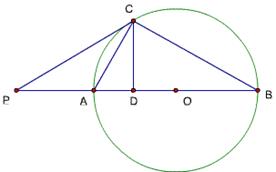
题目88
作图题：
已知两线段之和及积，求作这两条线段。
已知：两线段m和n
求作：两线段x及y,使x+y=m，xy=n^2

补个图（题88作法参考）
AD、BD即为求作线段x、y

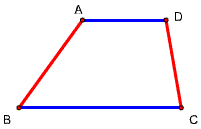
题目89（由题88变）
已知梯形ABCD如图，求作一直线平行于梯形的底边，且平分面积。

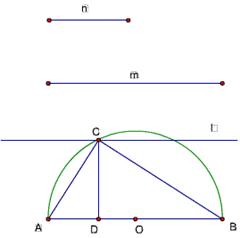
题目90
利用下图，证明：两个正数之和为定值，则这两个数相等时乘积最大。

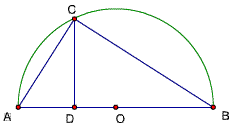
题目89作法：
如图，作两腰的延长线交于点O，作PB⊥AB使PB=OA，连结OP，
以OP为直径作半圆M，由圆心M作MN⊥OP，交半圆于点N，再以O为圆心ON为半径画弧交AB于点E，作EF‖BC交CD于F，则EF即为所求线段。

题91(题73变)
设a、b、c、d都是正数，满足a/b=c/d,且a最大，
求证：a+d>b+c

 

题92（人教版数学八年级下114页）
  在Rt△ABC中，∠ACB=90度，CD⊥AB，D为垂足，∠ACD=3∠BCD，E是斜边AB的中点，
∠ECB是多少度？

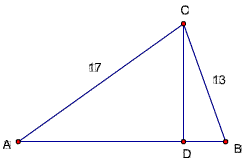
题93（题49变）已知，17cosA+13cosB=17,17sinA=13sinB,且∠A、∠B都是锐角，
求∠A/2+∠B的值。

 

题目93解：（构造法）
分别以17、13为边作△ABC，使AC=17，BC=13，CD为AB边上的高，
在Rt△ADC中，AD=17 cosA，在Rt△BDC中，BD=13 cosB，
CD=17sinA=13sinB
而AB=AD+DB=17cosA+13cosB=17，
∴AC=AB, ∠B=∠ACB,
∴∠A+2∠B=180度
∴∠A/2+∠B=90度。

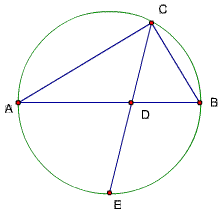
题94
已知如图，△ABC的∠C的平分线交AB于D，交△ABC的外接圆于E，
若CD·CE等于△ABC面积的2倍
求证：∠ACB=90度

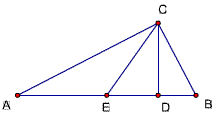
题目95
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，CM平分∠ACB 交AB于M，若AC>BC
求证：∠DCM=1/2·（∠B-∠A）

题目96
已知，△ABC中，∠ACB=90度，CD⊥AB，D为垂足，CE为AB边上的中线，且DE=DC，
求△ABC中较小的锐角的度数。

题目97
已知，△ABC中，∠ACB=90度，CE平分∠ACB 交AB于E，且EC+BC=AC，
求AC/BC

题97解：
设BC=a,AC=b,过点E作EH‖BC交AC于点H，作EF‖BC交BC于点F，
则四边形CHEF为正方形，设EH=x.则CE=√2x,
由AH/EH=AC/BC，得(b-x)/x=b/a, x=(ab)/(a+b)
由题意得，a+√2x=b
∴x=(b-a)/ √2a,
∴(ab)/(a+b)= (b-a)/ √2a,
得b^2-√2ab-a^2=0
b/a=(√2+√6)/2
即AC/BC=(√2+√6)/2

题目98
已知，△ABC中，∠ACB=90度，两直角边的差为2√2，
CD⊥AB，D为垂足，BD-AD=2√3，
求△ABC中的三边长。

 

题目99
圆内接三角形ABC中，直径AB=4，AB边上的高CD=2√3，
求∠A的度数。

题目100
已知，△ABC中， CD⊥AB，D为垂足，∠B=2∠A
求证：CB=AD-BD

题目101
已知，AB是⊙的直径，AB=4， D是OB的中点，过点D的弦CE⊥AB，
求弦CE的长。

（题54的解答）
已知如图，
⑤、AF=2EF
②、AC⊥CE
③、CB=BE
④、CF⊥AB
求证：
①、AC=CE
⑥、∠ABC=∠EBF

证明：
过点E作EM⊥CF如图，由△ADF∽△EMF得AD：EM=AF：FM=2
又BD为△CEM的中位线，则BD：EM=1：2
∴AD：DB=4：1=AC^2:CB^2
∴AC：CB=2：1
又CB=BE
∴AC=CE  (再由51的解答即有∠ABC=∠EBF成立)

题55的解答
已知如图，
①、AC=CE
⑤、AF=2EF
③、CB=BE
④、CF⊥AB
求证：
②、AC⊥CE
⑥、∠ABC=∠EBF
证明：过点E作EM⊥CF，如图
由△ADF∽△EMF得AD：EM=AF：FM=2
又BD为△CEM的中位线，则BD：EM=1：2
∴AD：DB=4：1
不妨设DB=x，CD=y,则AD=4x，
由勾股定理得AC=√[（4x）^2+y^2],BC=√（x^2+y^2）
又AC=2BC，得y^2=4x^2
即CD^2=AD·DB
CD：AD=DB：CD，∠ADC=∠CDB=90度
∴ Rt△ADC∽Rt△CDB
∴∠ACD=∠CBD
又∴∠BCD+∠CBD=90度
∴∠BCD+∠ACD=90度，
即∠ACB=90度(再证∠ABC=∠EBF成立)

题目102
初中三年级中考复习平面几何证明题一题多解

如图：已知青AB=AC，E是AC延长线上一点，且有BF=CE，连接FE交BC于D。求证：FD=DE。

分析：本题有好多种证明方法，由于新课标主要用对称、旋转方法证明，但平行四边形的性质、平行线性质等都是证题的好方法，我在这里向初中三年级同学面对中考需对平面几何证明题的证明方法有一个系统的复习和提高。下边我将自己证明这道题的方法给各位爱好者作以介绍，希望各位有所收获，仔细体会每中方法的异同和要点，从中能得到提高。我是一位数学业余爱好者，不是学生，也不是老师，如有错误，请批评指证。信箱：

 

证法一        ∧≌∠⊥∥△□°

 

证明：过E点作EM ∥AB交DC延长线于M点，则∠M=∠B，又因为∠ACB=∠B

∠ACB=∠ECM=∠M，所以CE=EM，  又EC=BF   从而EM=BF，∠BFD=∠DEM

则△DBF≌△DME，故  FD=DE；

证法二  

证明：过F点作FM∥AE，交BD于点M，

则∠1=∠2 = ∠B   所以BF=FM，

又  ∠4=∠3  ∠5=∠E

所以△DMF≌△DCE，故 FD=DE。

 

 

 

 

 

 

证法三

 

以BC为对称轴作△BDF的对称△BDN，连接NE，则△DBF≌△DBN，DF=DN，BN=BF，NF⊥BD，∠FBD=∠NBD，又因为∠C=∠FBD

所以∠NBD=∠C。  BN∥CE，CE=BF=BN，所以四边形BNCE为平行四边形。故NF∥BC，

所以NF⊥NE，因FN衩BD垂直平分，故D是FE的中点，所以FD=DE。（也可证明D是直角△NEF斜边的中点）。

证法四：

证明：在CA上取CG=CE，则CG=BF，

AF=AG，所以FG∥DC，又因为∠1=∠2，所以FBCG为等腰梯形，所以

FG∥DC，故DC是△EGF的中位线。所以

FD=DE。

 

证法五

证明：把△EDC绕C点旋转180°，

得△GMC，则△EDC≌△GMC

CE=GC=BF

连接FG，由于GC=BF，从而AF=AG，∠1=∠AFG

FG∥BC，所以FBMG为等腰梯形，所以

FG∥DC，故DC是△EGF的中位线。所以

FD=DE。

证法六

证明：以BC为对称轴作△DCE的对称△DCN，则和△DCE≌△DCN；CN=CE=BF

∠2=∠3；又∠1=∠3，∠B=∠1所以

∠2=∠B，BF∥CN，所以四边形BCNF为平行四边形，DC ∥FG，∠1=∠4，所以

∠2=∠4=∠CNG，所以 CG=CN=CE；

故DC是DC是△EGF的中位线。所以

FD=DE。

证法七

证明：延长AB至G，使BG=CE，又因AB=AC， BF=CE则AG=AE

  所以BC∥GE，则BD是△FGE的中位线。所以FD=DE。