数学破题36计第31计 解几开门 轨迹遥控
来源:未知发布时间:2017-06-24
第31计 解几开门 轨迹遥控?
●计名释义?
求动点的轨迹图形及轨迹方程是解析几何中的核心,体现了用代数方法研究几何问题的数学思想.轨迹是解析几何的灵魂,它就象一个遥控器,指挥着我们行动的方向.由方程研究曲线和已知曲线求其方程是解析几何的两大研究方向,在图形与方程问题遇到困难的人,往往疏忽了“轨迹”二字.正是“轨迹”二字告诉了动点的性质,动点的性质才是图形性质和方程性质的根基.??
●典例示范?
【例1】
动椭圆过定点M(1,2),以y轴为准线,离心率e=![]() . (1)求动椭圆左顶点的轨迹方程;(2)求椭圆长轴长的最大值和最小值.?
. (1)求动椭圆左顶点的轨迹方程;(2)求椭圆长轴长的最大值和最小值.?
【思考】 如M(1,2)为右顶点,则左顶点为?P(1-2a,2).?椭圆中心为(1-a,2),左准线为y轴.?∴![]() -a=0,?而e=
-a=0,?而e=![]() .
∴
.
∴![]() =2,有-3a+1=0,a=
=2,有-3a+1=0,a=![]() .
得点P1(
.
得点P1(![]() ,2);如M(1,2)为左顶点,有?P2(1,2),?∴P1P2中点为(
,2);如M(1,2)为左顶点,有?P2(1,2),?∴P1P2中点为(![]() ,2).?
,2).?
由以上可以预见,所求轨迹是中心为O′(![]() ,2)的椭圆.?
,2)的椭圆.?
【解答】 (1)设椭圆左顶点为M(x,y),则左焦点为F(x0,y0)=F(x+a-c,y),?
∵e=![]() ,且左准线为y轴,
∴
,且左准线为y轴,
∴![]() =0,?
=0,?
得a=x,c=![]() =
=![]() ,有:F
,有:F![]() ,由椭圆第二定义:
,由椭圆第二定义:![]() = e=
= e=![]() .?
.?
∴
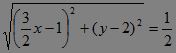 ,化简得:
,化简得:![]() ①?
①?
(2)椭圆①的长半轴a′=![]() ,∴-
,∴-![]() ≤x-
≤x-![]() ≤
≤![]() ,得x∈
,得x∈![]() .?
.?
原椭圆长半轴为a=x,∴2a=2x∈![]() .?故原椭圆长轴最大值为2,最小值为
.?故原椭圆长轴最大值为2,最小值为![]() .??
.??
【例2】 已知双曲线的两个焦点分别为F1,F2,其中F1又是抛物线y2=4x的焦点,点A(-1,2),B(3,2)在双曲线上,(1)求点F2的轨迹方程;(2)是否存在直线y=x+m与点F2的轨迹有且只有两个公共点,若存在,求出实数m的值,不存在,说明理由.?
【思考】 F1(1,0)为定点,∴|AF1|=2![]() =|BF1|为定值,设F2(x,y),则|F2A|-2
=|BF1|为定值,设F2(x,y),则|F2A|-2![]() =±(F2B-2
=±(F2B-2![]() ).得|F2A|=|F2B|或|F2A|+|F2B|=
4
).得|F2A|=|F2B|或|F2A|+|F2B|=
4![]() ,知动点F2的轨迹为直线AB的垂直平分线或以A、B为焦点的椭圆.?
,知动点F2的轨迹为直线AB的垂直平分线或以A、B为焦点的椭圆.?
【解答】 (1)点F2的轨迹方程为直线l:x=1或椭圆![]() .(不含短轴两端,即不含(1,0),(1,4)解法略).?
.(不含短轴两端,即不含(1,0),(1,4)解法略).?
(2)如图,当椭圆与直线y=x+m相切时,直线与所求轨迹恰有两交点(-为切点,另-为切线与直线x=1的交点),其他情况下,若直线y=x+m过椭圆短轴端点时与所求轨迹仅有一个公共点,若不过短轴两端点而经过椭圆内部时则有三个公共点,由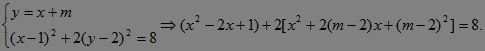
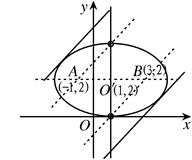 ?∴3x2+(4m-10)x+2m2-8m+1=0.?
?∴3x2+(4m-10)x+2m2-8m+1=0.?
此方程应有相等二实根,
∴Δ=(4m-10)2-12(2m2-8m+1)=0.?
化简得:m2-2m-11=0,∴m=1±2![]() .?
.?
【小结】 探求轨迹,一要注意
其完备性也就是充分性:只要符合
条件的点都适合轨迹方程;二要
注意其纯粹性也就是必要性:只要
适合轨迹方程的点都符合轨迹条件. 例3题图
以例2为例:若忽视了直线x=1(不含(1,0),(4,0))则不完备,若不除去(1,0),(4,0)则又不纯粹.??
●对应训练?
1.已知双曲线过坐标原点O,实轴长为2,其中一个焦点坐标为F1(6,0),另一个焦点F2为动点.?
(1)求双曲线中心的轨迹方程;?
(2)双曲线离心率最大时,求双曲线方程.?
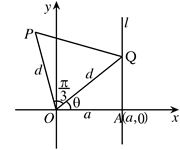
2.已知定直线l和线外一定点O,Q为直线l上一动点,△OQP为正三角形(按逆时针方向转),求点P的轨迹方程.?
3.已知双曲线过坐标原点O,实轴长为2,其中一个焦点坐标为F1(6,0),另一个焦点F2为动点.(1)求双曲线中心的轨迹方程;(2)双曲线离心率最大时,求双曲线方程.?
4.已知抛物线C:y2=4x,(1)若椭圆左焦点及相应准线与抛物线C的焦点及相应准线分别重合.(1)求椭圆短轴端点B与焦点F所连线段的中点P的轨迹方程;(2)若M(m,0)是x轴上的一个定点,Q是(1)中所求轨迹上任意一点,求|MQ|的最小值.??
●参考答案?
1.设F2(x0,y0), ∵O(0,0)在双曲线上,?
∴|OF2| - |OF1| =±2,|OF1|=6,?
∴|OF2|=6±2,如|OF2|=8,则x20+y20=64 ①?如|OF2|=4,则x20+y20=16 ②?
当O、F1、F2共线时,F1、F2应在点O两侧,故上述轨迹中应分别不含(8,0),(4,0)?设双曲线中心为M(x,y),则?
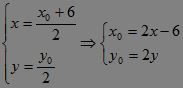 ③?
③?
③代入①:(2x-6)2+(2y)2=64, 即(x-3)2+y2=16(x≠7)?
③代入②:(2x-62+(2y)2=16, 即(x-3)2+y2=4(x≠5)?
(2)∵a=1,∴e=![]() = c,且c=|MF1|=
= c,且c=|MF1|=![]() ,?
,?
如M的轨迹为(x-3)2+y2=16,
则c=![]()
∵-4≤x-3<4,∴-1≤x<7?
当x=-1时,cmax=7.?
如M的轨迹为(x-3)2+y2=4,则![]()
∵-2≤x-3<2,∴1≤x<5,当x=1时,cmax=5,?
于是取c=7,a=1,∴b2=48,又当x=-1时,由(x-3)2+y2=16,得y=0,即双曲线中心为(-1,0),一个焦点为F1(6,0),故实轴在x轴上,则所求方程为:(x+1)2-![]() =1.?
=1.?
2.如图作OA⊥l于A,以直线OA为x轴,
 过O且垂直于OA的直线为y轴建立
过O且垂直于OA的直线为y轴建立
如图的直角坐标系,设A(a,0),则有
直线l:x=a,设|OQ|=|OP|=d
∠AOQ=θ,则∠AOP=θ+![]()
设P(x,y),∵d=![]() ,
,
∴x= d cos (θ+![]() )=
)=![]() (
(![]() cosθ-
cosθ-![]() sinθ)
第2题解图
sinθ)
第2题解图
?=![]() (1-
(1-![]() tanθ),?
tanθ),?
y=dsin(θ+![]() )=
)=![]() (
(![]() sinθ+
sinθ+![]() cosθ)=
cosθ)= ![]() (tanθ+
(tanθ+![]() ).?
).?
于是得点P的参数方程: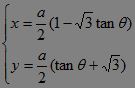 (θ为参数) 消去参数得:x+
(θ为参数) 消去参数得:x+![]() y=2a.
y=2a.
3.(1)设F2(x0,y0),∵O (0,0)在双曲线上,∴|OF2| - |OF1|=±2,|OF1|=6,∴|OF2|=6±2,如|OF2|=8,则x20+y20=64 ①;如|OF2|=4,则x20+y20=16 ②,当O,F1,F2共线时,F1,F2应在点O两侧,故上述轨迹中应分别不含(8,0),(4,0).?
设双曲线中心为O′(x,y),则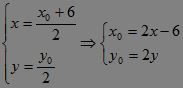 ③?
③?
③代入①:(2x-6)2+(2y)2=64, ?即 (x-3)2+y2=16 (x≠7).?
③代入②:(2x-6)2+(2y)2=16, 即 (x-3)2+y2=4 (x≠5).?
(2)∵a=1,∴e=![]() = c,且c=|MF1|=
= c,且c=|MF1|=![]() ,?
,?
如M的轨迹为(x-3)2+y2=16,?
则c=![]() .?
.?
∵-4≤x-3<4, ∴ -1≤x<7,?
当x= -1时,cmax =7.?
如M的轨迹为(x-3)2+y2=4,则c=![]() .?
.?
∵-2≤x-3<2,∴1≤x<5当x=1时,cmax =5.?
于是取c=7,a=1. ∴b2=48,又当x= -1时,由(x-3)2+y2=16,得y=0,即双曲线中心为(-1,0),一个焦点为F1(6,0),故实轴在x轴上,则所求方程为:(x+1)2![]() =1.?
=1.?
4.(1)如图设椭圆中心为O′(x?0,0),
 由于左焦点F(1,0),左准线x= -1,
由于左焦点F(1,0),左准线x= -1,
∴x0=c+1,且x0+1=![]() .?
.?
∴a2=c(x0-1)=x20-1,
b2=a2-c2=(x20-1) - (x0-1)2=2x0-2,
得椭圆短轴端点B(x0,![]() ).?
第4(1)题解图
).?
第4(1)题解图
设FB的中点为P(x,y),则:?
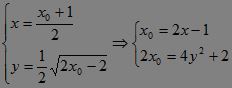 消去x0:y2=x-1(x≥1).?
消去x0:y2=x-1(x≥1).?
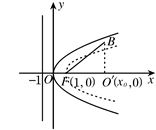
(2)曲线y2=x-1(x≥1)的图形如图中虚线所示,其顶点为F(1,0).?
显然当m≤1时,|MQ| min=1-m,即点M(m,0)到抛物线顶点F最近,当m>1时,以M(m,0)为圆心,R为半径的圆的方程为:?(x-m)2+y2=R2.(*)?
由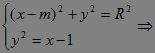 x2+(1-2m)x+m2-1-R2=0.?
x2+(1-2m)x+m2-1-R2=0.?
命Δ≥0,即(1-2m)2-4(m2-1-R2)=0,?
∴R2≤![]() .
(1)?
.
(1)?
当m≥![]() 时,R min=
时,R min=![]() ,?
即|MQ|的最小值为
,?
即|MQ|的最小值为![]() .?
.?
当1<m<![]() 时,不等式(1)无解,说明圆(*)与抛物线y2=x-1不可能有交点,此时抛物线顶点与M距离最近,即|MQ| min=m-1.?
时,不等式(1)无解,说明圆(*)与抛物线y2=x-1不可能有交点,此时抛物线顶点与M距离最近,即|MQ| min=m-1.?
注:此题选自陕西师大“中学数学教学参考”04·1~2期P72,63题,原题答案为:
当![]() ≤1,即m≤
≤1,即m≤![]() 时,|MQ|无最小值;当
时,|MQ|无最小值;当![]() >1,即m>
>1,即m>![]() 时,?|MQ| min=
时,?|MQ| min=![]() .笔者以为不妥,故重解如上,不当之处,请各位同仁指正.??
.笔者以为不妥,故重解如上,不当之处,请各位同仁指正.??
更多精彩文章
- 高中数学:求切点弦所在直线方程的方法
- 高中数学攻略:椭圆、双曲线、抛物线的重点知识归纳和常用结论
- 2017高考数学 直线与圆的方程
- 高考数学:椭圆、双曲线、抛物线的重点知识归纳和常用结论
- 数学破题36计第16计 摆渡开门 萍水相逢
- 高考数学难点突破25圆锥曲线综合题
- 高中数学所有公式 考点难度超级合集!
- 高考金钥匙数学解题技巧大揭秘专题十六 椭圆、双曲线、抛物线
- 2017年高考数学提分秘籍,导数方程不能解三种破解策略
- 高一|高中数学:圆的标准方程
- 高考复习:6个妙招帮助女生有效提高数学成绩
- 高考数学复习:高考数学题中的惊人发现!
- 数学指导:判断充分与必要条件的常用方法
- 高考数学复习:数学高考冲刺复习要点谈
- 高一数学经验速递:你必须反省的几个问题