数学破题36计第16计 摆渡开门 萍水相逢
来源:未知发布时间:2017-06-25
第16计 摆渡开门 萍水相逢?
●计名释义
有道数学题,求证π>![]() .
很多学生不知所措时,却有一学生说此题非常简单,不过需找个第三者. 现在他已经指定了一个第三者,就是整数3.?
.
很多学生不知所措时,却有一学生说此题非常简单,不过需找个第三者. 现在他已经指定了一个第三者,就是整数3.?
因为π>3,又3>![]() ,所以π>
,所以π>![]() .?
.?
这里的第三者,如同一个渡船,它能把“无关”的两岸经过自己连接起来.这就是数学上的“过渡法”,它是一个“三者牵线,截迂为直”的策略,在不等式中具体表现为传递法.?过渡法所用的渡船形式多样,可以是参数,可以是图形,当然也可以是函数、方程、不等式等.?
●典例示范?
【例1】
已知曲线C :![]() ,求曲线C关于直线x-y+1=0的对称曲线C1的方程.?
,求曲线C关于直线x-y+1=0的对称曲线C1的方程.?
【分析】 一般解法为“轨迹转移法”:(1)设P(x, y)是C1上的动点;(2)求出P(x, y)关于直线x-y+1=0的对称点Q(x′, y′), (3)将Q点坐标代入C的方程;(4)用x,y表示x′,y′,即得C1的方程.?
此法甚繁,考虑到这里的对称轴直线的斜率为1,因此可以直接从中得到替换式.?
【解答】 由x-y+1=0得![]() 代入C的方程得
代入C的方程得![]()
即得C1的方程得![]() ?
?
【点评】 对称轴x-y+1=0本为一条参照定位直线,现在拿来充当替代式,成了名符其实第三者“摆渡”.??
【例2】 长为2的线段AB在抛物线y=x2上滑动,求AB中点的轨迹方程.?
【解答】 设A(x1,y1),B(x2,y2)为抛物线y=x2上两点,那么:?
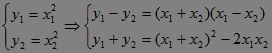
?设AB中点为M(x,y),那么: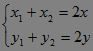 ,
,
有: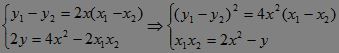
?∴|AB| 2=(x1-x2)2+(y1-y2)2 =(1+4x2)(x1-x2)2 =(1+4x2)[(x1+x2)2-4x1x2]?
=(1+4x2)[4x2-4(2x2-y)]?
已知|AB|=2.
∴(1+4x2)(y-x2)=1?所求点M的轨迹方程为:y=x2+![]()
【点评】 本解说明:当直线与曲线相交,若已知弦的长度,而目的是求弦中点的轨迹,可以对其两端的坐标实施“设而不求”.??
【例3】
椭圆![]() (a>b>0)的右准线是x=1,倾斜角为α=
(a>b>0)的右准线是x=1,倾斜角为α=![]() 的直线l交椭圆于A、B两点,已知AB的中点为M
的直线l交椭圆于A、B两点,已知AB的中点为M![]() .?
.?
(1)求椭圆的方程;?
(2)若P、Q是椭圆上满足|OP|2+|OQ|2=![]() 的两点,求证:|kOP·kOQ|为定值.?
的两点,求证:|kOP·kOQ|为定值.?
【分析】 按常规,应设直线的斜截式方程,并代入椭圆方程,用韦达定理依中点的条件先求直线的截距而后确定椭圆方程.这样也算设而不求,可这种方法计算量仍然太大.?
请欣赏如下解法:?
【解】 (1)椭圆的右准线为x=1,即![]() ?∴a2=c,b2= a2-c2
= c-c2.?
?∴a2=c,b2= a2-c2
= c-c2.?
所求椭圆应为:![]() 也就是 (1-c)x2+y2=
c(1-c) ①?
也就是 (1-c)x2+y2=
c(1-c) ①?
设弦AB的两端分别为A(x1,y1),B(x2,y2),则:?
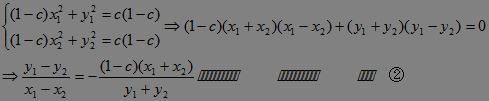 ??
??
∵kAB=![]() ,又AB中点为M
,又AB中点为M![]() ,∴x1+x2=-1,y1+y2=
,∴x1+x2=-1,y1+y2=![]()
以上全代入②:1=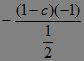 ,?
∴1-c=
,?
∴1-c=![]() ,c=
,c=![]() ,代入①:
,代入①:![]() x2+y2=
x2+y2=![]()
所求椭圆方程为:2x2+4y2=1.?
(2)由(1)知椭圆方程:2x2+4y2=1. 设P、Q的坐标依次为(x1,y1),(x2,y2).?
有: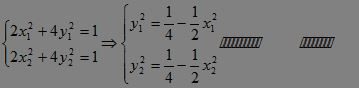 ③
③
?∴|OP|2+|OQ|2=![]() ,?
∴(x
,?
∴(x![]() +y
+y![]() )+(x
)+(x![]() +y
+y![]() )=
)=![]() ④?
④?
③代入④:x![]() +x
+x![]() +
+![]() -
-![]() (x
(x![]() +x
+x![]() )=
)=![]() ,?
,?
∴x![]() +x
+x![]() =
=![]() .?
.?
∵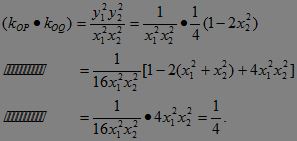
故|kOP·kOQ|=![]() 为定值.?
为定值.?
【点评】 本解的优点是:?
1.为确定椭圆方程,须求两个参数a与b,这里先由准线的条件归为只须求一个参数c;?
2.无论求椭圆方程或证斜率之积的绝对值为定值,都需要利用弦AB或PQ的端点,这里只是抽象的设定而并不真的去求它,在解题过程中都自然地逐一消失,使“设而不求”的技术达到最佳效果.??
【例4】 (05湖北卷21题)设A、B是椭圆3x2+y2=λ上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.?
(Ⅰ)确定λ的取值范围,并求直线AB的方程;?
(Ⅱ)试判断是否存在这样的λ,使得A、B、C、D四点在同一个圆上?并说明理由.?
【分析】 (1)已知弦的中点求弦所在直线的方程,故(1)可以实施“设而不求”;(2)判断“四点共圆”的最佳方法,是引入平面几何的相应知识.?
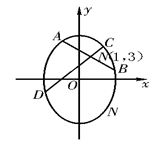 【解答】 (1)∵点N(1,3)在椭圆3x2+y2=λ内,
【解答】 (1)∵点N(1,3)在椭圆3x2+y2=λ内,
∴3·12+32<λ,即λ>12,∴λ∈(12,+∞).?
设AB两端点为A(x1,y1),B(x2,y2),则有:?
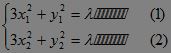
(1)-(2):3(x1-x2)(x1+x2)
+(y1-y2)(y1+y2)=0 (3)?
∵N(1,3)是线段AB的中点,∴x1+x2=2,y1+y2=6. 代入(3):? 例4题解图
6(x1-x2)+6(y1-y2)=0,于是kAB=![]() ,故直线AB的方程为:y-3= -(x-1),即x+y-4=0.?
,故直线AB的方程为:y-3= -(x-1),即x+y-4=0.?
(2)解法1:CD为AB的垂直平分线,且kAB=-1,∴kCD=1,直线CD:y-3=1·(x-1),即x-y+2=0.直线AB的参数方程方程是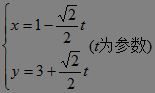 :?
:?
∴代入椭圆方程得: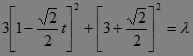 ,即2t2+12-λ=0.(由(1)知λ>12),设此方程之二根为tA,tB,则tA·tB =
,即2t2+12-λ=0.(由(1)知λ>12),设此方程之二根为tA,tB,则tA·tB =![]() ?
?
直线CD的参数方程方程是: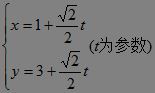
代入椭圆方程得: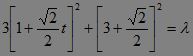 ?,即2t2-6
?,即2t2-6![]() t+12-λ=0.
t+12-λ=0.
设此方程之二根为tC ,tD ,则tC·tD=![]() ?
?
由(4),(5)知|tA·tB|=|tC·tD|,也就是│AN│·│BN│=│CN│·│DN│,这就是说,存在λ>12,使得A、B、C、D四点总在同一个圆上.??
【小结】 按理说,解数学题避免不了“求”,其最终目的(不论是计算题还是证明题),都是要“求”出最后的结果的.这里说的“不求”,专指可以简化的解题中间过程,用“设”去代替“求”.?
从宏观上说,“设而不求”是解析几何解题的基本手段.“设而不求”的灵魂是通过科学的手段使运算量最大限度的减少.因此需要做到:(1)凡是不必直接计算就能更简洁的解决问题的,都尽可能实施“设而不求”;(2)“设而不求”不可避免的要设参,消参.而设参的原则是宜少不宜多.(3)“设而不求”的思想还可以应用到三角、立几、代数等数学的其他领域中去,限于篇幅,这里不再多讲.有心的读者,不妨在解题中留心运用.??
●对应训练?
1.长为2的线段AB在抛物线y=x2上滑动,求AB中点的轨迹方程.?
2.求过圆x2+y2-2x=0和直线x+2y-3=0的交点,且和直线x+3y-4=0相切的圆的方程.?
3.已知直线y=-x+1与椭圆![]() (a>b>0)交于A、B两点,且线段AB的中点在直线
(a>b>0)交于A、B两点,且线段AB的中点在直线
l:x-2y=0上.(1)求此椭圆的离心率;(2)若椭圆的右焦点关于直线l的对称点在圆x2+y2=4
上,求此椭圆的方程.?
4.已知![]() ,(a>0,a≠1,x>0),判断f (x)的单调性,并证明你的结论.?5.如图,已知直线l:x-ny=0(n∈N),
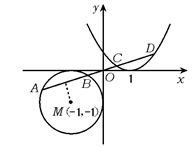
,(a>0,a≠1,x>0),判断f (x)的单调性,并证明你的结论.?5.如图,已知直线l:x-ny=0(n∈N),
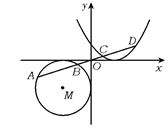 圆M:(x+1)2+(y+1)2
=1,
圆M:(x+1)2+(y+1)2
=1,
抛物线φ:y=(x-1)2,
l交M于A、B,
交φ于C、D,
求![]() 第5题图
第5题图
●参考答案?
1.无须设直线的点斜式解方程组.设A(x1,y1),B (x2,y2)为抛物线y=x2上两点,那么:?
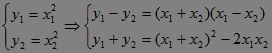
设AB中点为M(x,y),那么: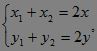
有: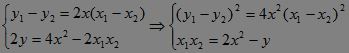
∴|AB| 2=(x1-x2)2+(y1-y2)2 =(1+4x2 )(x1-x2)2?
=(1+4x2)[(x1+x2)2-4x1x2]?
=(1+4x2)[4x2-4(2x2-y)]?
已知|AB|=2.
∴(1+4x2)(y-x2)=1? 所求点M的轨迹方程为:y=![]()
2.无须求直线与圆的交点.设所求圆的方程为:x2+y2-2x+λ(x+2y-3)=0.?
即x2+y2+(λ-2)x+2λy-3λ=0 ①?
此圆的圆心为D![]()
半径R=![]()
∵直线x+3y-4=0与圆相切.?
∴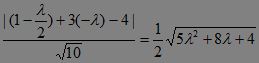
化简得:λ2-4λ+4=0,∴λ=2.?
代入①:x2+y2+4y-6=0 ②?
②即为所求圆的方程.?
3.无须先求直线与椭圆交点的坐标.
由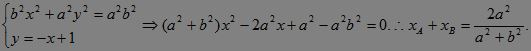
得AB中点为M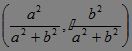 ,?
,?
∵点M在直线x-2y=0上,?∴a2=2b2. 即 a2=2(a2-c2),∴a2=2c2, e=![]()
容易求得F(c,0)关于直线l:x-2y=0的对称点为?F′![]() .??
.??
代入x2+y2=4,得 c2 = 4,从而a2=2c2=8,b2=c2=4.?
则所求椭圆方程为 ![]()
4.无须先求函数的解析式.
设?logax=t,则x= at,(t∈R).?原函数式变形为:f (t)=![]() 或
或![]() (x∈R).?
(x∈R).?
∵![]()
这里a≠0,无论a>1或0<a<1都有f ′(x)>0,故f (x),从而原函数在其定义域内是增函数.?5.无须分别求直线与曲线
 的交点再求弦长,
的交点再求弦长,
如图,圆心M(-1,-1)到直线
x-ny=0的距离为:![]()
∴|AB|
2=(2![]() 2=
2=![]()
由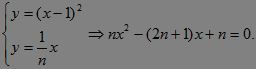 第5题解图
第5题解图
设此方程之二根为xC ,xD,则?
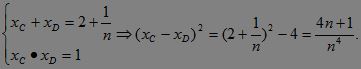
|CD|2=(xC - xD)2+(yC - yD)2=![]()
于是: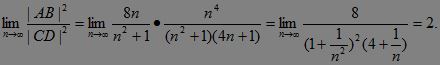
更多精彩文章
- 高中数学:椭圆焦半径的几种求解方法
- 高中数学:求切点弦所在直线方程的方法
- 高中数学攻略:椭圆、双曲线、抛物线的重点知识归纳和常用结论
- 2017高考数学 直线与圆的方程
- 高考数学:椭圆、双曲线、抛物线的重点知识归纳和常用结论
- 高考数学难点突破25圆锥曲线综合题
- 高考数学难点突破40探索性问题
- 高中数学之椭圆习题精选(手抄版)
- 高中数学所有公式 考点难度超级合集!
- 高考金钥匙数学解题技巧大揭秘专题十六 椭圆、双曲线、抛物线
- 高考复习:6个妙招帮助女生有效提高数学成绩
- 数学指导:判断充分与必要条件的常用方法
- 高一数学经验速递:你必须反省的几个问题
- 高考数学复习:数学高考冲刺复习要点谈
- 高考数学复习:高考数学题中的惊人发现!